Three equations are unbearable

Written article | Hemanth

Translation | C & C

Review | zhenni

On the left, the Niccolò Fontana, also known as Tartaglia. He contributed to Gerolamo Cardano in solving the problem of the cubic equations, but also became an enemy on this road.

Historically full of competition: Edison and Tesla, Harding and Kerrigan (both ice athletes) and so on. In the 16th century Italian mathematician Caldano and Nicolo Fantama (the latter's wider name is Taltalia, which means "oxy", because the face was injured by the French soldier's sword when he was a teenager, he spoke. The conflict between the name) is also dramatic. The cause is: three equations.

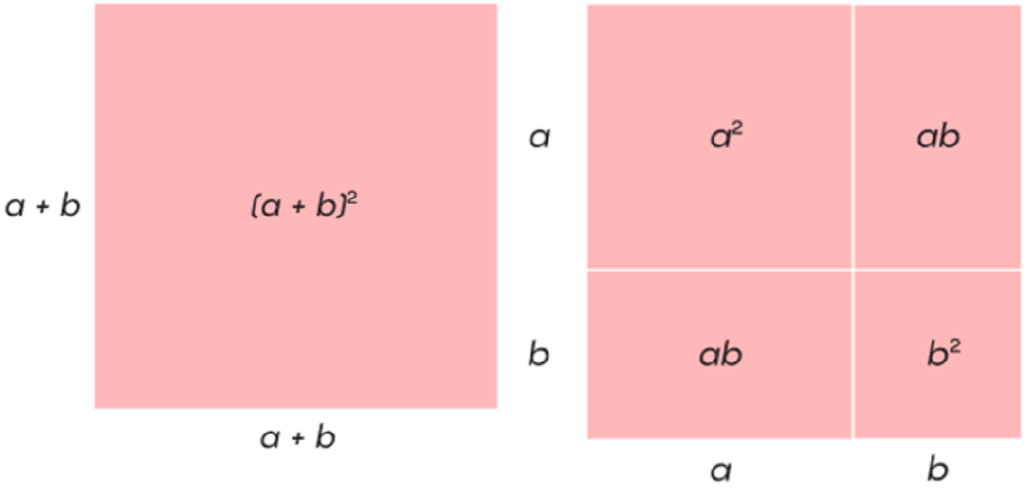
Most high school students know how to solve the secondary equation, such as x2-x-3 = 0. AX2+BX+C = 0 The solution of the equation, or the root is:

Is there a similar formula for the equation that is higher (more power in X)? In essence, before Caldano, Taltalia, and their contemporaries, they already had the task of solving this problem.

The modern algebra of the above abstract symbol expression and the familiar operation method can be traced back to the 17th century, which is a long time later than these scholars' times. However, the thinking of algebraic ideas, as well as the ability to solve the linear and secondary equations we think, has been developing slowly in the past thousands of years.

In the 16th century, the algebraic equation is still expressed by text rather than symbols. All coefficients must be non -negative because the number

Similarly, the cube with the side length to T can be decomposed into 6 square blocks to have the following expression:

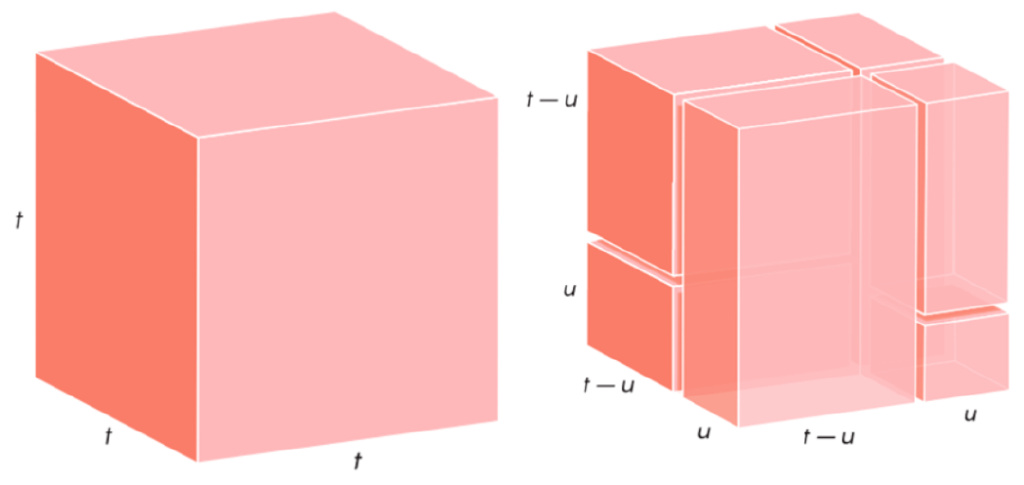
(T> u).

Scipione Del Ferro was a professor at the University of Bologna in the early 16th century. He was the first person to make significant progress in solving three equations. Unfortunately, due to the strange academic secret culture at the time, we did not know all his achievements. Scholars will not rush to publish their own research results, nor will they be intoxicated to prove an recognition of a theorem or solve a problem. They will challenge each other and carry out "mathematical duel": sending each other with challenges, who will solve the most the most, who can solve the most the most. , Whoever wins. The winners often get career development and more students. Therefore, these discoveries are sometimes stored and become secret weapons used in the competition in the future.

When C and D are positive, Fero can solve the equation of x3+cx = d. Three equations that do not have a square item like this are called "DePRESSED CUBIC". Although mathematicians in the 16th century will not use this expression, Fero proves that one of the roots is:

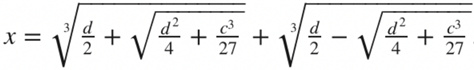
This modern formula is suitable for any deficit cubic equation, but because the three equations of different coefficient symbols are considered different issues, Fero's solution cannot be directly applied to other losing cubic equations. We only know that Fero solved these three square roots because he taught this technology to his student Antonio Fior, and the latter boasted that he could solve such equations after Fero's death.

At the same time, Taltalia, who was self -taught, discovered another form of three equations -by subtracting linear item CX. This laid the foundation for the mathematical duel between Fiolol and Taltalia. In 1535, they exchanged 30 problems, and the deadline was one and a half months. Taltalia provides Flor a variety of problems, and Flor, who is weaker mathematics, uses the strategy of "all eggs are placed in a basket", and raised Taltalia Three losses of three equations. Just a few days before the deadline, Taltalia came up with ways to solve these problems and completed all problems within two hours; at the same time, Florol did not solve any problems. The news of Taltalia's success spread throughout Italy, and the humiliated Phiol also disappeared from people's vision.

The general view at that time was that it was impossible to solve the cubic equation, so Taltalia's achievements shocked Caldano.

Caldano was a highly sought -after doctor at the time, but he was irritable, gambling, struggle with his son who was inconsistent with his behavior, jail in the religious referee, and so on. He was troubled by one after another. However, he still contributed to mathematics, medicine, philosophy, religion, music and physics. Decades later, Gottfried Leibniz wrote, "Caldano is a great person because he has the shortcomings; if there are no shortcomings, he will be unparalleled." His works are 7000 pages, including the first serious research on probability theory.

Caldano tried to copy the success of Taltalia on the cube, but failed, so he began to stress to persuade Taltalia to share his method, and even vowed to promise to keep confidential:

I vowed to you with the belief of my gentleman as a gentleman. If you tell me your discovery, I will never announce it, but as a real Christian, I promise to record them with a password. This way, no one can understand after my death.

In the end, in 1539, Taltalia compromised and shared his techniques for solving the three equations of losses with Caldano. Although there is no complete proof, for the smart Caldano, it is enough to find this method to discover the potential mathematical principles. Soon after, Caldano could solve any three equations for any loss. He observed this replacement: Although he vowed to Taltalia, Caldano told him the talented assistant Ludovico Ferrari. He was just a servant of Caldano at first, but in the end, he could sit up with Caldano mathematically. By helping Caldano to study the three equations, he was very proficient in algebra and found how to simplify the four equations (one yuan and four times) into three equations. Therefore, Caldano and Ferrari can solve any four or less equations.

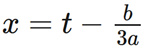
Caldano recognized the importance of these achievements and urgently hoped to announce these results. But they all grown from the seeds of Taltalia, and this will violate his vow.

In 1543, during a Bologna journey, Caldano saw in the manuscript of Fero that he earlier the three equations of losses than Taltalia. In Caldano's view, the discovery lifted his obligation to Taltalia. Two years later, Caldano published "ARS Magna", including him and Ferrari's research on three and four equations.

Although Caldano acknowledged Taltalia's work in the book, he was furious, accusing Caldano theft and violating the sacred vows. Caldano left these accusations to his loyal attack dog Ferrari. The fierce debate lasted for several months in the form of a public booklet, which led to the mathematical duel between Taltalia and Ferrari, and eventually conducted an open debate in Milan, Ferrari. Taltalia is more willing to fight with the respected Caldano, but was rejected. Although there are very few retained details, the attack on Taltalia is very fierce, especially in the noisy people of the opponent's hometown. When he continued the debate the next day, Taltalia disappeared because he had left Milan.

Ferrari received a large number of work invitations, and Taltalia's reputation was destroyed. Although Taltalia has many significant achievements in addition to those achievements related to the three power, he has no text and no one in his death when he dies; but Caldano has received eternal reputation, many people, many people, many people, many people, many people, many people, many people, many people, many people, many people The publication of "Dabu" marks the beginning of modern mathematics.

In 1824, Niels Abel proved this fact for the first time, which was nearly three centuries later than "Dapua". In 1830, the 18 -year -old political instigator Evariste Galois expanded this work by giving the exact standards for the solution to the order polynomial. Although Galova died in a duel two years later (with guns instead of math duel), his contribution to mathematics was huge.

The results of these "impossible" are not the ending of the story. Mathematicians are still studying polynomials, their roots and properties. David Hilbert raised a well -known question about seven multiple root roots in 1900. It was considered solving in the 1950s, and now it has attracted people's interest. It is speculated that modern mathematicians can make new progress on this issue, and there is no need to repeat competition around three times.

This article is authorized to reprint from the WeChat public account "Institute of Physics of the Chinese Academy of Sciences", editor: zhenni.

Original link:

https://www.quantamagazine.org/the-scandalous-History--the-Cubic-Formula-20220630/

Special Note

1. Enter the "Boutique Column" at the bottom menu of the WeChat public account of the WeChat public account.

2. "Returne" provides a monthly retrieval article function. Pay attention to the public account and reply to the year+month for the four digits, such as "1903", you can obtain an index of articles in March 2019, and so on.

- END -