Forbidden cauliflower, retina and coffee pot baby

First of all, what are the similar points in the three things in the title?

Maybe most people think that this question is similar to how "Zen and Motorcycle Maintenance Technology" are connected together, or similar to Hawking's classic paragraphs in "The Big Bang".

Of course, what we want to discuss is not Zen or homophonic stalks (after all, what kind of broccoli can only be homophonic Bladeli), what to discuss is actually the similarity of these things in shape characteristics. As for you, you have to tell me that these three things will make people crazy -for example, a myopia child who does not like to eat cauliflower is boiled coffee to yourself -my evaluation is:

After all, I can’t say you are wrong, right?

What are these three things (cauliflower, retinal blood vessels, coffee pots) in the shape of these three things? Of course, it is difficult to see that it is a bit difficult at a glance. Take the first player cauliflower as an example. If there is no impression in your mind, take a look at the picture below:

Every time I eat spicy spicy food, I must order dishes

Remove the green leaves, and when a small piece of broccoli is put down, you will find that this small piece of broccoli is very similar to the previous large pieces of broccoli -almost narrowed the version of the cauliflower. In other words, broccoli is similar to part of it.

I don't think the life of cauliflower is incomplete (big fog)

Of course, it is impossible for the biological world to have such a perfect similarity, but this does not prevent us from abstracted this situation and strictly, that is, the object is similar to that of its own. This nature is called "self -similarity". There is a professional player in broccoli. Its shape is very close to this rigorous definition, which is the famous Roman broccoli.

It is said that there is a commonly known as Qingsheng Pagoda. I think Fahai can use this town Bushi (Bushi)

OK, we can now say that a more significant characteristics of a broccoli have been found. So is the retina and coffee pot? For retina retinal, it seems to be able to analogize. Although it is not as good as that of broccoli, it is very similar to that of broccoli, but for the continuous split of retinal blood vessels, each smaller fork and the previous fork seem to have similar places. It is called self -similarity.

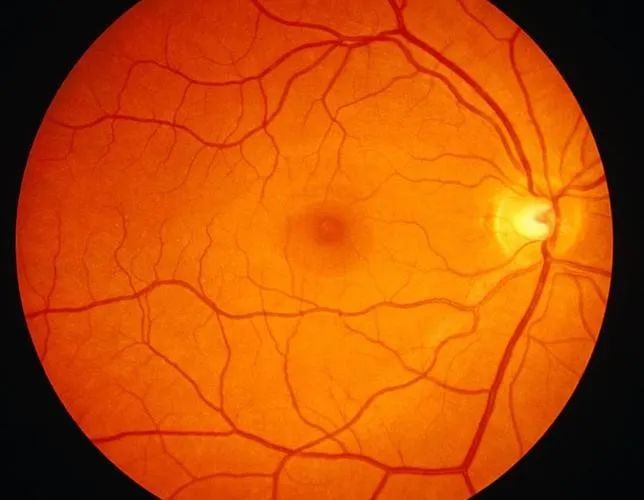
Slawed children's shoes are recommended not to watch ~~

As a result, through the analogy of the first two things, we first came to a class of objects with a special nature: they are similar to some of them, that is, they are similar. We can construct such graphics ourselves. For example, take a solid -edge triangle, divide the connection along the three sides into four small triangles, and then remove the small triangle in the middle. Finally, repeat this process of the remaining three small triangles. "Serbisky Triangle". Each of it is exactly similar to itself.

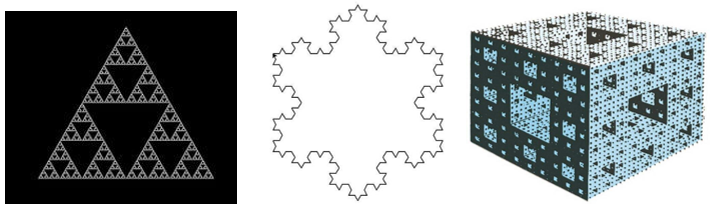
The Serbisky triangle, as well

In theory, you can construct a lot of strange graphics in this way. This kind of graphic should have a door class to include them. In fact, there are such categories. This is the definition of the fractal that most people come into contact with, that is, the fractal is a geometric object with similarity, or the self -similarities under the transformation of the label. The introduction of fractal is attributed to the famous mathematician Mandelbrot.

Benoît B. Mandelbrot (1924-2010), Polish mathematician.

In fact, as early as the nineteenth century, mathematicians have constructed some "pathological" graphics. For example, in 1883, Contol constructed the famous "Contel Three Settings". But in the concept of traditional physics, smooth or regular things are natural products. According to the idea of ​​calculus, as long as the division is small enough, everything is smooth, so the morbid graphic is not within the scope of research. Mungolu Luo pointed out: "The floating clouds are not spherical, the peak is not a cone, the coastline is not a circle, the bark is not smooth, and the lightning never travels along the line." In 1982, he created the word "FRACTAL". This was born. The division has "fractal dimensions", for example, the dimension of Koch Snowflake is about 1.262.1.262 is greater than 1 and less than 2, so the length of the Koch snowflake is infinitely long and the area is zero.

From this perspective, cauliflower and Mungolur are indeed a little bit of heart. (Stranger)

In fact, Wudo has a stricter definition of fractal. The nature of "self -similar" is okay but unnecessary. Munbroben means dealing with rough things. For example, you must have heard the story of "the United Kingdom's coastline is infinite", and it is difficult to tell the British coastline. But we can also calculate the dimensions of the British coastline (in fact about 1.21). In addition, the line segment is also self -similar under a certain division method, which does not show that the line segment is also divided.

The rigorous definition of the divided into division is: the graphics of the Housedorf dimension than the topological dimension. The number of topological dimensions is always integer, but the number of Masdorf can take all the positive numbers. As for what the number of Masdov dimensions is, this is the theory of measurement. In general, due to the accuracy of actual objects (after all, the magnification is limited, the British coastline cannot be magnified to the atomic scale). It is a good way to calculate the capacity dimension to calculate.

The specific calculation method refers to Teacher Zhao Kaihua's "New Concept Physics · Hoting" (don't ask, ask the author is lazy) for non -strict and similar fractures like the British coastline. Therefore, it is also called "random fractal". The retinal vascular is actually a free -scale example. The computer can describe natural phenomena by adopting a certain random growth model. The most classic model is called Diffusion-Limited Aggregation (DLA). Many biological phenomena can be explained by DLA models. The specific generation method is as follows: Place a static particle in the center of the two -dimensional square point as a genetic seed, and then randomly release a particle to walk randomly from a far -long boundary. If this particle goes to the neighboring position of the static particles, stops and bonded to form a gathering collective. When this particle is bonded or out of the boundary, a particle is released from the boundary, and the steps of the above are repeated. It can be proved that this model has statistically self -similarity. If you choose a different radius R as a circle within this group, it can be found that the number of particles contained in the circle is proportional to the 1.6th side of the 1.7 side of R. This shows that the DLA model is 1.6 ~ 1.7.

Disvoading limit gathering model (above) and some examples

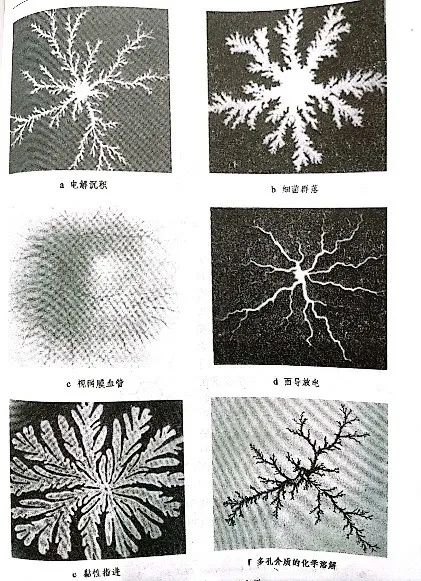
Picture source: Zhao Kaihua Luo Weiyin's "New Concept Physics · Hoting" second edition P256 and P257

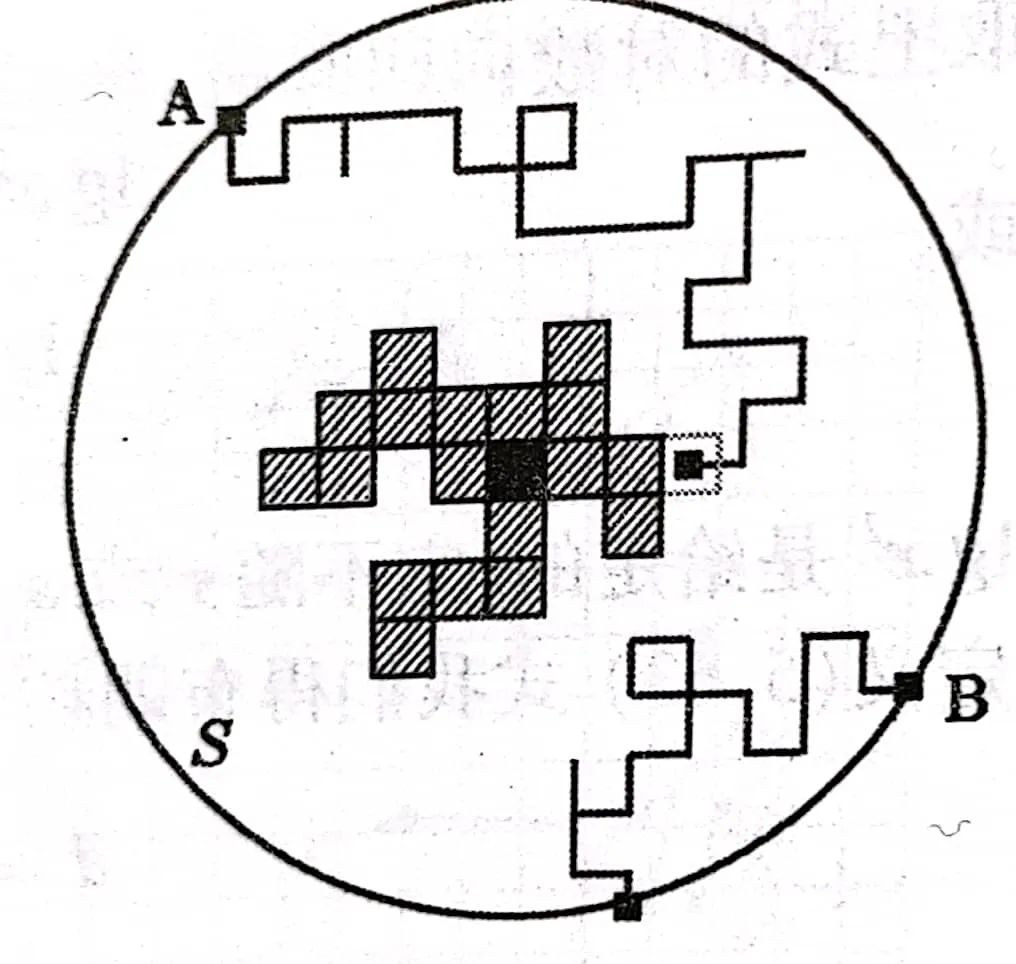
Having said so much, we seem to forget the No. 3 player coffee pot. What is it? The key to cooking coffee is the filtration structure in the coffee pot. The coffee residue inside can be abstracted into a two -dimensional honeycomb structure. But what does this have to do with the shape?

Filtering structure and two -dimensional honeycomb

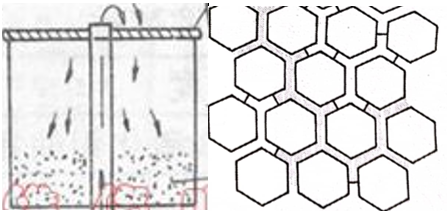
It turns out that the penetration of coffee from the coffee residue is random, just like a valve with a random switch between honeycomb. Such a model is called "over-infiltration model" by mathematician Hammersley, and the excessive model is seized (at the apex), the key is over-infiltration (the valve is at the channel) and the more complicated seat-key Over infiltration. It can be imagined that the random switch of the valve will affect the rate of coffee flowing out, and when the valve is closed enough, the coffee cannot flow out, which has undergone essential changes. Through some specific analysis of the valve kick -up rate, it can be found that it has statistically divided properties. Over -penetration model is an important type of computer fractal model, which has important applications when dealing with secondary phase changes. For example, studying the flow of fluids in porous media, random formation of stars in spiral galaxies, quarks in nuclear substances, non-closed transformations, and even sociological phenomena can be studied.

Knowledge of not cold or hot: Brown movement is also randomly divided (can't think of it)

Because of the extensive existence of fractal, this discipline has been full of vitality since its founding. It is foreseeable that with the development of science and technology, it has a broad prospect for fractal and related science.

references:

Zhao Kaihua and Luo Weiyin. New Concept Physics · Freshology [M]. Second edition. Higher Education Press, 2005.

Yang Zhanru. Fractal physics [M]. The first edition. Shanghai Science and Technology Education Press, 1996.

[3blue1bRown. (2017, march 6). [Official bilingual] Forming is not necessarly similar. Https:////video/bideo/bv1wx411c7wt?spm_Id_Id_Id_Id_Source=05884343434343434343434343434333.

Author | University of Chinese Academy of Sciences 1902 Huayong Tong

Edit: lychee jelly

- END -