Is the hairdresser paradox a paradox?

Is the hairdresser paradox a paradox?

Written article | Wenlan (Academician of the Chinese Academy of Sciences and Professor of Mathematics at Peking University)

1 What is a paradox

We define the next "formula" to the paradox: paradox is a reasoning that leads to contradiction but unknown reasons.

According to this definition, once the cause of the contradiction is found, the paradox is no longer a paradox. In addition, the cause of contradictions should be more difficult to detect.

This meaning may be different from the definition of paradox in many literatures. The author advocates this definition.

2 hairdresser paradox

There is a hairdresser in a village who just gives people who do not make haircuts in the village. Does he give himself a haircut?

If he gives himself a haircut, he is a hairdresser for himself. According to his principles, he should not make a haircut for himself. contradiction.

If he does not give himself a haircut, he is a person who does not give himself a haircut. According to his principles, he should make a haircut for himself. Also contradictory.

This is a well -known and very interesting reasoning. Due to the contradictory reasons, this reasoning is called "hairdresser paradox".

But can't really find the reason for contradictions?

The purpose of this article is to explain that in fact, the cause of this contradiction is not difficult to detect, so the paradox of the Taler is not enough to be called a paradox.

3 Solution of hairdresser paradox

Let's describe the hairdressing paradox again:

There is a hairdresser in a village, just to give the village who do not make a haircut for their haircuts. Does he give himself a haircut?

If he gives himself a haircut, he is a hairdresser for himself. According to his principles, he should not make a haircut for himself. contradiction.

If he does not give himself a haircut, he is a person who does not give himself a haircut. According to his principles, he should make a haircut for himself. Also contradictory.

If this time it is not easy to see the reason for contradictions, please note that in the second statement, the third word "yes" in the first statement was replaced with "existence". Others did not move.

Is it easier to see the contradiction?

Yes, it should be said that it is easier to see such a change. The reason for the contradiction is to assume the existence of such a hairdresser. Therefore, this contradiction is nothing more than a hairdresser with this nature (that is, the people who do not give their haircuts for their own haircuts) in the village do not exist in the village.

The cause of the contradiction was found, and the paradox was not a paradox, and the problem was solved.

4 text game?

But how do you find the reason for the contradiction? We replaced "yes" with "existence". Is this a text game, whether the concept of stealing the concept, is it changed the problem?

of course not. "Yes" means "existence". Instead of "existence" with "existence", it has not changed the problem, but the words are more scientific and eye -catching, making people notice that there is a hypothesis of "existence" hidden here.

Assuming, or premise, it is crucial to reasoning. Knowing that there is assumptions, it will not be a fuss when the contradiction is introduced, and it means that the assumptions are incorrect. But if you do n’t know that there are assumptions, you will be unable to explain the contradiction, and you will be exclaimed as a paradox. Therefore, don't lose or blur any assumption.

5

It is said that the hairdresser paradox is solved. However, people may not be relieved, and the problem is too easy to crack: just changed the word "existence", which inspired and caused the answer. This answer is too bland.

In order to let people completely believe that this answer is not plain at all, the problem is indeed in existence. Let us quote the scriptures and review the theorem of the founder of the collection theory. For this reason, we must first review the concepts of the collection theory: the set of mapping, full shots, and subsets.

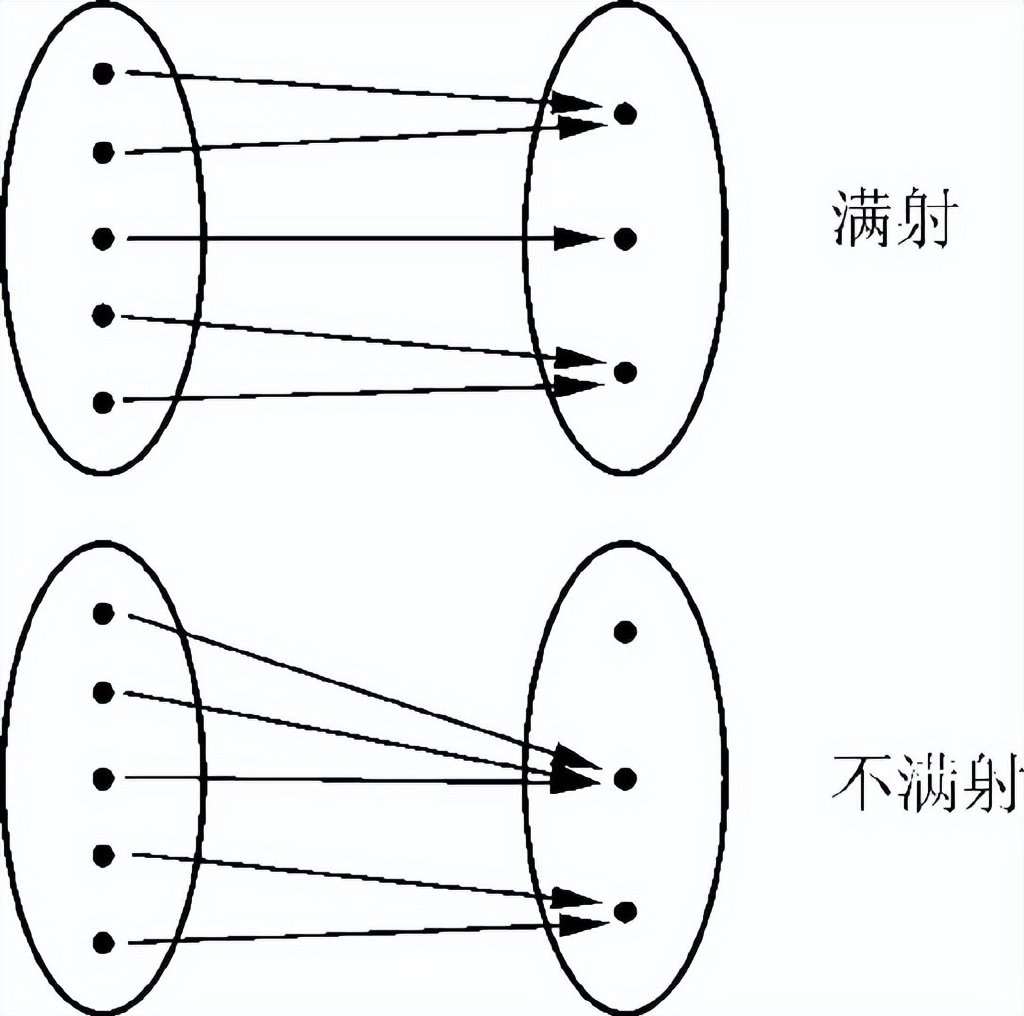
Let X and Y be two episodes. The so -called mapping F: X → Y from X to Y refers to a rule that specifies the only element in each x in X. This is the only element specified in X called the image under X, which is recorded as f (x). Called x is the doctrine of the mapping, Y is the value domain of mapping. If each element in the value domain y is defined as a image of a certain element in the domain X, it is called F to be full. as the picture shows:

We also need a concept: the set of subsets. Let X be a set. Use p (x) to represent the set of all subsets of the set x. For example, if x = {1, 2, 3}, then

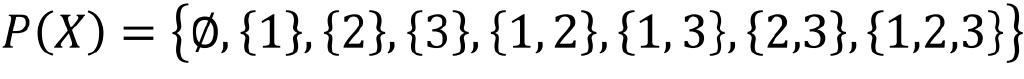
6 Kangtu Ding Theory

Kangto theorem does not have a full shot from X to P (x) to any set x.

Prove any mapping f: x → p (x). The prove that F is not full. For this order

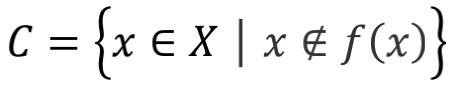
Let's prove that there is no Z明x, so that f (z) = c.

For this reason, use anti -syndrome. Assuming Z 使x exists, f (z) = c. So,

If z ，c, then z∉f (z). But f (z) = c, so z∈c. contradiction.

If z ，c, then z∈f (z). But f (z) = c, so z∉c. Also contradictory.

This shows that there is no Z 使x, which makes f (z) = c. Therefore, F is not full, and Kang Tuding has obtained a testimony.

The theorem of Kangto is one of the earliest and most important theorems. The beauty of this theorem can probably represent the wisdom of human beings. This theorem is generally put in the third -year course "Real Change Function" of the Department of Mathematics, but it has almost no basic knowledge. It is what middle school students can understand and appreciate. The statement of the Cog's theorem generally is generally, "there is no one to one -to -one from X to P (x)", but there is actually no full shot. Of course, there is no one -to -one correspondence without full shots.

7 Comparison of Kangto theorem and hairdresser paradox

What is the relationship between Kangto theorem and hairdresser paradox? Let's explain to the "haircut" to the Coto theorem. Use the collection of people in the village. For each villager X, F (X) indicates the collection of those who are hairdresser in the village, that is, the "customer set" of X. Then the collection of Kangto considers

There is no Z∈x, so that f (z) = c. The language of translation into a haircut is:

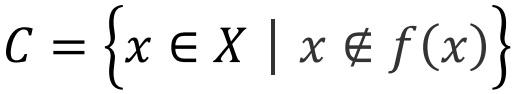
There is no such hairdresser in the village, which gives people who do not make haircuts in the village. This is a profound fact that Kangto proves.

Let's translate the process of Kangto's reasoning into the language of a haircut:

If z ，c, then z∉f (z). But f (z) = c, so z∈c. contradiction. (If he gives himself a haircut, he is a person who has a haircut for himself. According to his principles, he should not give himself a haircut. Contradiction.)

If z ，c, then z∈f (z). But f (z) = c, so z∉c. Also contradictory. (If he does not give himself a haircut, he is a person who does not give himself. According to his principles, he should give himself a haircut. It is also contradictory.)

It can be seen that the barber reasoning is Kangto pushing.

8 reviews

So, why is the paradox of Kangto theorem and the hairdresser one of the theorem and one is a paradox?

Kangto clearly wrote that the existence of such a Z is just a hypothesis. So it was not surprised to introduce contradictions, but immediately concluded: there is no such Z.

The hairdresser's paradox has blurred the "existence" of the scientific language in daily language. After "existence" was replaced by "yes", it unknowingly changed from assumptions to natural righteousness, so the contradiction could not be explained, and it became a "paradox". It can be seen that we have replaced "You" into "existence" in front, which is indeed not a text game. The issue of the hairdresser's paradox is indeed in existence.

But say "change back", right? Who first?

Kang Tuding theorem (1895), a hairdresser paradox (1907), Kang Tuo is first. Therefore, it is right to say "replacement".

Kang Toto deeply proves that there is no such weird hairdresser. Twelve years later, the hairdresser's paradox took care of the inference process of Kangto, but it blurred the sexual assumptions of Kangto, which caused the contradictions to be unable to explain and "paradox".

Isn't this like a prank?

9 About Russell Paradox

Readers may know Russell's paradox and have heard of "the popular version of Russell Paradox". As mentioned above, the hairdresser's paradox is almost a prank to the theorem of Kangto. What about Russell paradox?

This question is left to readers to track and think best. But rushing to know that the answer is the excellent nature of human beings, so it is also briefly explained: Russell Paradox (1902) is obviously inspired by the theorem of Kangto, but it is very different from the hairdresser's paradox. Its assumptions were much hidden, so that the collection theory at the time could not be noticed. Of course, the assumption was completely cracked by the later collection theory, so Russell Paradox is no longer a paradox. However, Russell's paradox greatly stimulated the collection theory at the time, which was of great significance to the progress of collection theory.

[Postscript] In fact, how much "paradox" such as hairdressing paradox can be solved is how much is a prank of the theorem of Kangto. For example, "I just love those who don't love themselves", "I hate those who do not hate themselves", "just show those who do not praise themselves", "just criticize those who do not criticize themselves", "just repair those who do not repair those who do not criticize themselves." Repair your own robot "," Just quote those books that do not quote your own ", and so on. As one of these "anti -body and proves", the haircut is just a particularly vivid image.

About the Author

Wenlan (1946-), graduated from the Department of Mathematics Mechanics of Peking University in 1969, and received a master's degree in Peking University in 1981. The mentor was Mr. Liao Shantao. He received a doctorate in Northwestern University in 1986, and the mentor was Professor R. Williams. From 1988-1990, he worked in postdoctoral research at Peking University and stayed in school. Wen Lan is mainly engaged in research on the differential power system. It is important to make important issues to make important issues such as C1 closed theory, C1 connection theory, stability guessing, star flow problem, Palis dense guessing, etc. Contribution; won the Chen Provincial Mathematics Award in 1997, was elected as an academician of the Chinese Academy of Sciences in 1999, was elected as an academician of the Third World Academy of Sciences in 2005, and won the Hua Luogeng Mathematics Award in 2011.

This article is compiled based on the public report of Academician Wenlan at Shuangliu Tanghu Middle School. The original text was published in the 12th Issue of 2011, the original title "Kangtuo theorem and Barber Paradox".

Produced: Popular Science China

- END -