Can we hear the shape of the drum?

Previously, we made a "sound of sound" in the live broadcast of the week, that is, seeing the shape of the sound, where we tried to see the resident wave formed by a dimension of the ultrasonic generator, and we also saw the formation of the two -dimensional metal board formed. The resident wave (that is, Kraney graphics).

Specific diagram of ultrasonic sound suspension, picture source network

Kraney graphics, map source network

But no matter what, it is to fix the geometric shape of the device first, and then consider what kind of sound (vibration) can produce this geometric shape, then some people with a big brain may ask: What will happen in turn? Can we judge the geometric shape of the sound device through sound?

In fact, this problem has a more concise and more widely circulated version: Can we hear the shape of the drum? (Can One Hear the Shape of a Drum?) And this is also the title of the famous article in 1966 in the 1966. In order to consider this issue mathematically, we must re -express the problem.

What is a drum?

First of all, what kind of equation description of a drum surface is described? We can imagine that a membrane stretches on a rigid stand, which forms a two -dimensional drum. The vibration of this two -dimensional drum is described by the volatility equation. At the same time, because the edge of the drum surface is firmly pasted on the rigid shelf, we can think that the boundary condition of the fluctuation equation is the boundary condition of the Dilixre. If we use function f (x, y, t) to describe the offset of the dots at the position of the drum at the position (x, y) at the time of the Z direction, then the fluctuation equation of the drum can be written.

Separate variable f = u*exp (IΩt), and the cost of cost

Among them, u (x, y) is the offset of the drum in the Z direction. V is the wave speed of the drum surface. Here is an irrelevant constant. ω is the frequency of vibration, and γ is the boundary of the drum. In order to simplify our mark, we can think that the equation of our research has the following form:

Among them, ω indicates the inside of the drum, the λ is the original value of the Lapras operator, which corresponds to the frequency of the drums mentioned earlier. Then, the mathematical "listening to the drum discrimination" can be expressed. If we know all the signs of a certain drum, can we only determine the shape ω and γ of the drum.

So the question raised by mathematicians is that if we know the frequency of all the vibrations of a drum, can we only determine the shape of the drum?

Drum area

Before revealing the answer, let's put our attention in the article of KAC 1966, and see what interesting results can some physical intuition bring us? As KAC mentioned in his article, the issue of the value of the Lapras operator in a certain area can be traced back to the era of WEYL. If we give a λ, consider that the value of this sign is less than λ The number of one, that is, consider the function

Weyl proves that when λ → ∞,

This means that if we know all the frequency of the drum, we can at least know the area of ​​the drum. Let's observe the result of Weyl a little carefully. The distribution of the values ​​of the Laplas operator on a drum. When the value of this sign is large, it is distributed in the interval of the interval [λ, λ+dλ]. The number of values ​​is proportional to the area of ​​the drum, and it has nothing to do with the λ, and it has nothing to do with the shape of the drum.

Next, I will show that we can use a physical comparison to "demonstrate" the theorem proved by Weyl. First of all, I want to emphasize that the problem of "listening to drums" is actually the issue of the Laplas operator in a region. It not only appears in the fluctuation equation, but also in quantum mechanics Schrindinger equation and diffusion equations. Among these different physical problems, the proliferation problem is the easiest to provide us with physical intuition about the distribution of the Laplas operator's original value distribution. Therefore, we want to focus on how to draw inspiration from the diffusion equation to get "listening to drum discernous discernous discernous discernous discernous discerning discrimination Part of the answer to the question.

First of all, the diffusion equation is to describe the partial differential equation of the diffusion phenomenon, and the diffusion phenomenon is roughly said that over time, the material will spontaneously spread from the high concentration to the place where the concentration is low. If we use the function

To describe the concentration of the substance at the time T and the position R, then this function will meet the diffusion equation:

And there are boundary conditions

And initial conditions

By separating variables, we can get the value of our familiar value

as well as

At present, intuitively, for a very small time T, the particles of the diffusion substance do not have enough time to feel the impact of boundaries. Therefore, we expect to have

in

Still meet the same diffusion equation and the same initial conditions, but this time there is no restrictions on other conditions (such as limits of boundary conditions). The only thing that needs to be satisfied is that the concentration of the material needs to be greater than equal to 0, that is, P₀≥0.

In this case, the display expression about P 表 is the famous Gauss distribution,

Therefore, according to our judgment above, when T → 0, there should be

If this formula is also right at the position r = 在, we can get it

If we go further, make points on both sides of the upper formula, and use the natural conditions

Available

Note that the upper form can be written in the following form,

in

Then at this time, if we apply Hardy-LittleWood Karamata Tauberian theorem (the content of this theorem will be explained at the end of the text), we can get it and this is the result of Weyl (γ (2) = 1).

The above is not strictly argued based on the physical analogy. Of course, we can strictly use the above discussion in mathematical language, but this is beyond the goals of this article. Interested readers can directly read the original text of KAC. In short, we can now confirm at least we can hear the area of ​​drums.

Other information

But can we hear more information? In fact, we can use the same analogy to continue to consider this matter. Assuming that in the diffusion problem, the place where the material is concentrated at the beginning is very close to the boundary, that is, the ρ in our initial conditions is very close to the boundary of the region. In a very short time T, the boundary condition formed by a straight line should be very good (as shown in the left picture below),

So we can get it,

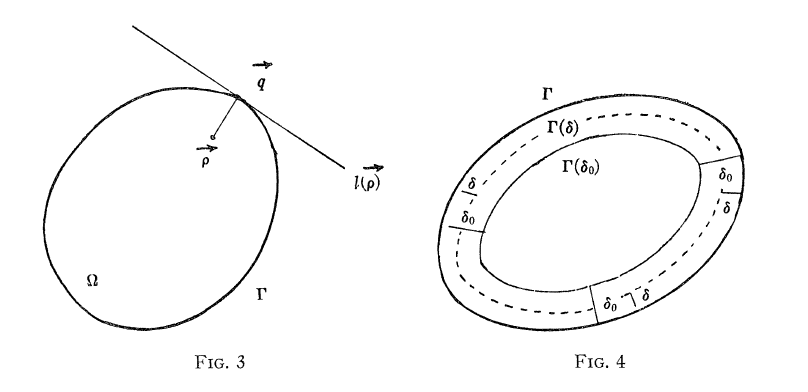
Among them

Among them, Δ is the shortest distance from 界 to boundary γ. For points, the attenuation of the upper mode will only contribute only very close to the border. With a little calculation, the following formula can be obtained.

The first item on the right is the result we got at the beginning, and the index attenuation that can tell us the circumference information of the boundary, that is, we can hear the length of the drum!

Can we still hear more things? In fact, for convex multilateral drums, KAC has obtained the following formulas.

Among them, θ 多 is every angle of polygon. If this polygon has N bars, and if we let N → ∞ make each θ₀ → π, then the constant of the upper type will become

This seems to be that the constant items given by smooth drums are the same, and we cannot distinguish the drum through the constant item. What will happen to the drums of Fu Liantong? If we let all polygonal shapes close to the smooth curve, the result is that the constant item will become (1-R) ​​1/6, of which R is the number of holes in the drum surface. Therefore, it is natural to speculate that we have

In other words, we can also hear the touches of the drum (that is, the number of drums)!

The above is the main conclusion in KAC's 1966 article. In this article, KAC also shows that he is not clear about the ultimate answer to "listening to drum discrimination". Until 1992, Carolyn Gordon, David Webb, and Scott Wolpert constructed a pair of areas with different shapes but the same value according to the Sunada method. These areas are concave polygon. The two areas have the same characteristic values ​​to prove the symmetry of the Laplas operator. BUSER and others have promoted this idea, and they have built many similar examples. Therefore, the answer to the KAC question is: For many shapes, people cannot fully hear the shape of the drums. However, as KAC's original article, we can infer some drum information.

On the other hand, Steve Zelditch proves that if you have restrictions on certain convex plane areas with analytical boundaries, the answer to the KAC question is yes.

The inverse examples of Gordon, Webb, and Wolpert, the drums of two different shapes have the same frequency of this sign. Note that these two drums have the same area and circumstances. [3]

In reality, because the tone of the drum is determined by the relative amplitude set of this vibration mode, it is not enough to have a set of exactly the same frequency of this signs. For each model, they also need to have the same relative amplitude, which may not be easy to achieve in reality.

In addition, people cannot directly hear the vibration of the drum (tympanic membrane). On the contrary, our ears listen to the vibration of sound waves in the air, so we need to consider the spread of sound ... this will become more complicated. Therefore, in actual life, it seems difficult to find two different drums with the same sound.

Math supplement

Hardy-LittleWood Karamata Tauberian theorem, when Y → 0+, the two below AN are gradually undergoing

Feller derives a more general form about this theorem, considering the real -value function that has different boundary variability

(Here, only parts need to be bound to the difference: that is, each boundary sub -interval on [0, ∞) meets the boundary difference. However, at this time, more complicated additional assumptions need to be converged. )definition:

The theorem connects the approximateness of ω to the gradual approximation of F in the following ways. If ρ is non -negative, the following statement is equivalent.

Reference materials:

[1] KAC, M. (1966). Can One Hear the Shape of a Drum? The American Mathematical Monthly, 73 (4), 1–23. Https://doi.org/10.2307/2313748

[2] Can We Hear the Shape of a Drum? | Comsol Blog [3] Hearing the Shape of a Drum -Wikipedia

[4] Hardy – Littlewood Tauberian Theorem -Wikipedia

Edit: Mu Zi

- END -