From a mathematical perspective, what is the "dimension" of the second dimension?

Now I write in front of the desk, reach up to turn on the table lamp, and I can take out the pen from the drawer. When I stretched out my arms forward, a strange little statue brushed the fingertips, it was the lucky symbol given to me by my sister, and reached back, the tentacle was a black cat curled on my back. On the left is a stack of bills and letters that must be processed, and on the right is the research notes of my article. Upper, lower, front, back, left, right: In this three -dimensional personal world, the coordinate axis is projected into me through the straight structure of the office. It is defined by three connected straight corners, just like most Western buildings Same.

Our architecture, education and dictionary tell us that space is three -dimensional. "Oxford English Dictionary" defines the three -dimensional space as "an unsatisfactory continuous area ... has three dimensions: height, depth and width, and everything exists and moves." As early as the 18th century, Emmanuel · Kant (Immanuel Kant) believes that the three -dimensional European space has innate inevitability, and as the computer -generated image and video games continue to occupy today's people's lives, we are also constantly affected by the impact of the right -angle coordinate grid that seems to have already axioms. Essence From the perspective of the 21st century, the three -dimensional special signs of the space seem to be even more self -evident.

However, a fundamental innovation of Western culture proposes the concept of any mathematical structure of our lives, which indicates that people's once inherent cognition of reality will be subverted. Although its birth is often described as a transition to describe natural phenomena to use mechanical theories, it can be said that modern science is more important, and of course it is longer. It is the conceptual change that causes us to regard space as geometric structure.

In the past century, the exploration of how to describe the geometric shape of space has become a major topic of theoretical physics. Starting from Albert Einstein, scientists tried Incurrence of space shape. Although we are accustomed to three dimensions in the local area, the general theory of relativity depicts the four -dimensional map of the universe, and the string theory says it has 10 dimensions -if you use an extended version called M the theory, there is some 11 dimensions. The M theory has many variants in the 26 dimensional space. Recently, its description of 24 dimensions has attracted great interest in theoretical mathematicians. But what are these "dimensions"? What does the 10 -dimensional space we are talking about mean?

In order to think about space in modern mathematics, we must first consider it as a field that material may occupy. At least, "space" must be considered something extended. Although this is obvious for us, Aristot is deeply hazy about this view, and his understanding of the material world has always been the mainstream of Western thought in the late classical era.

Strictly speaking, Aristotle's physics does not include spatial theory, only the concept of the location. For example, a cup placed on the table is surrounded by air for Aristotle, and the air itself is a material. In his world map, there is no so -called "empty", there is only one material -a cup, the boundary between the same material -air, the limit. The table can also be regarded as a substance. For Aristotle, "space" (if you want to call it this) are just the infinite limit between the cup and the material around it. Without the concept of extension, other substances cannot occupy it.

A few centuries ago in Aristotle, LeuCippus and Democritus was leaving Kobe and Demolutus. "Vision, that is, the material world is composed of small particles (that is, atoms) moved in the void. But Aristotle refused to accept the atomic theory, and he claimed that the concept of void was logically discorsed. Aristotle said that according to the definition, the void cannot "exist." How to refute Aristotle's denial of the concept of void and further denying of space ductility will be a huge project of several centuries. Until the early 17th century, Galileo and Descartes used the ductility of space as one of the cornerstones of modern physics, and this innovative vision was realized. As an American philosopher Edwin Burtt said, in the views of these two thinkers, "the concept of physical space is assumed to be the same as the concept of geometry" -tly Euclidean geometry.

Before physicists accepted the views of Eueal, the artists began to try to create a space concept in line with geometry. It was because of them that we realized this significant leap in the conceptual framework. In the late Middle Ages, Plato and Plato and Pythagoras, as Aristotle's main ideas, affected the birth and spread of a new view in Europe. This view is that when God created the world, it was based on the law of Euclidean. Therefore, if the artist wants to truly depict the world, he should follow the creator in the performance strategy. From the 14th century to the 16th century, Giotto, Paolo Uccello, Piero Della Francesca and other artists have developed a pivotal method. Technology -a painting style originally called "geometric drawing". Through consciously exploring the principles of geometry, these painters gradually learned how to build an image of objects in three -dimensional space. In the process, Europeans were influenced by them, and gradually began to understand the space of thinking in Europe. Samuel Edgerton, a historian, tells the extraordinary transition of modern science in the "Rate Heritage" (1991) in "Giotto Geometry" (1991). Out of overthrowing is a slow and indirect process. When people stand in front of the perspective painting, they instinctively feel that they seem to be "seeing" the three -dimensional world on the other side of the wall, and this transition is not easy to detect. When philosophers and primitive scientists are cautiously challenging Aristotle's precepts on space, artists have set up another unusual and more radical path by resorting to the senses of the senses in this field. Literally, perspective is a form of virtual reality. Like today's VR game, it aims to make the audience have an illusion that they have been transmitted to another geometric and psychological world. Essence

The structure of "real" has changed from a philosophical and theological problem to a geometric proposition

The illusion of the unreal Eujiridi space is gradually imprinted in the consciousness of Europeans, and this space is also regarded as the structure of the real world by Descartes and Galilei. It is worth adding that Galileo has received perspective training. His ability to depict in depth was prominent in his pioneering moon painting. The painting not only depicts the mountains and valleys, but also implies the same hard materials as the moon as the earth.

Through the spatial characteristics of perspective images, Galileo can deduct objects such as artillery shells to move according to the law of mathematics. Space is an abstraction -a void that has neither characteristic nor changing, neither touch nor perception. The only known attribute is its form of European. By the end of the 17th century, Isaac Newton expanded Galileo's vision to including the entire universe, and from then on a potential infinite three -dimensional vacuum -a huge, quality, never to each of each The virtual phenomenon extended in the direction, the structure of "real" has gradually shifted from a philosophical and theological problem to a geometric proposition.

In the past, the painters used mathematical tools to develop a new method of building images, and to the dawn of the "Scientific Revolution", Descartes discovered another method of image constructing a internalized mathematical relationship. In this process, he standardized the concept of dimension and injecting a new way to treat the world into the world, a new tool for scientific research.

Today, almost everyone can recognize his talent in the image of the Descartes plane -a rectangular grid marked with X and Y axis, and a coordinate system.

According to the definition, Descartes plane is a two -dimensional space because we need two sets of coordinates to calibrate one of them. Descartes found that through this framework, he can connect the geometric shape and equation. For example, a circle with a radius of 1 can be described with equation x + y = 1.

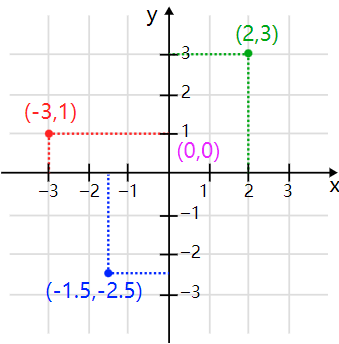
A large number of graphics that can be drawn on this plane can also be described by equations. In the further analysis of the exercise of physicists, this "analysis" method, that is, "Descartes Geometry", will become Newton and Leibniz development. The cornerstone of the calculus. One way to understand the calculus is to study the curve, which enables us to formally calibrate the steeper position of the curve and reach the position of the maximum or minimum value. It is applied to a motion research, and the micro -accumulation has become an analysis and prediction method. For example, it can analyze the conditions that the objects that are thrown into the air can reach the maximum required conditions. Specific speed. Calculus points have become a key tool for almost all scientific branches since the emergence.

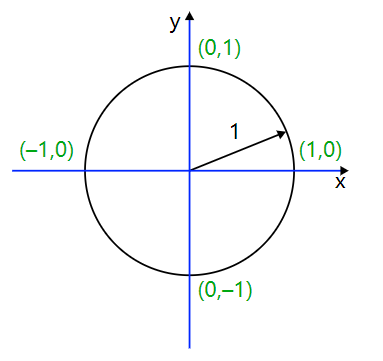
Taking the previous icons as an example, it is easy to add the third axis method. Therefore, with the X, Y, and Z axis, we can describe the surface of the sphere -such as the outer skin of a beach ball. The equation here (for a sphere with a radius of 1) becomes: x + y + z = 1

Through three axes, we can describe the shape in the three -dimensional space. Similarly, each point consists of three coordinates uniquely calibrated: this is a necessary condition for the "three -dimensional" constructing three -dimensional space.

But why stop here? What if the fourth dimension is added? Called this dimension as P. I can now write a equation for the so -called sphere in the four -dimensional space: x + y + z + p = 1. I can't draw this object for you, but it is reasonable to increase another dimension in mathematics. "Reasonable" means that there is no contradiction in doing so -there is no reason to do so. "Destination" has become a pure symbolic concept, and there is no inevitable connection with the material world.

A 'Dimension ’Becomes A Purely Symbolic Concept Not NECESSARILY Linked to the Material World At all.

We can continue to increase more dimensions. If a sphere is defined in a five -dimensional space, it has five coordinate axes (x, y, z, p, q), and you can get the equal formula: x + y + z + p + q = 1. In the six -dimensional space: x + y + z + p + q + r = 1, push according to this.

Although higher -dimensional spheres may be difficult to imagine, they can be described symbolically. One way to understand the history of mathematics is to gradually realize what seemingly obvious things can actually be surpassed. This is also what Charles Dodgson, also known as Lewis Corol, means in "Alice's Wandering Wonderland" (1871). "Six things that are impossible."

In mathematics, you can choose any dimension to describe a sphere. All I have to do is to continue to add new coordinate shafts, which mathematicians call it "freedom". According to conventions, they are named X, X, X, X, X, X, X, etc. Just as any point on the Descartes plane can be described by two (x, y) coordinates, and any point in 17 dimensions can be described with a set of 17 coordinates: (x, x, x, x, x, x , x ... x, x, x). In such a multi -dimensional space, the surface of this sphere is usually called manifolds.

From a mathematical perspective, one "dimension" is nothing more than another coordinate axis (another degree of freedom), which eventually becomes a pure symbolic concept that does not necessarily connect with the material world. In the 1860s, Augustus de Morgan, a logicist with innovative thinking, summarized the conclusion from the increasingly abstract viewpoint of this field, stating that mathematics is purely "symbolic science" Except for yourself, you don't have to be related to anything. In a sense, mathematics is the logic of all freedom in imagination.

Unlike mathematics that can be freely played in the field of ideology, physics is closely related to nature, at least in principle, it is linked to the material world. However, all this brings a more free possibility, because if mathematics allows more than three dimensions, and we think that mathematics has a role in describing the world, so why should the dimensions of the physical space be limited to only three in three. Woolen cloth? Although Galileo, Newton, and Kant all believe that the length, width and height choices are self -explanatory, does our world not have more dimensions?

Once again, the concept of the universe with more than three dimensions is also through the art medium. In most cases, literary speculation is infused with public consciousness. Among them, the most famous of which is the "Plane of Edwin A Abbott) of mathematician Edwin A Abbott National "(1884). This fascinating social satirical novel tells the inconspicuous square story living on the plane. The existence of three -dimensional one day, the Lord of the Sphere, visited him and brought him into the magnificent solid world. In this three -dimensional paradise, the square saw its own three -dimensional version, cube, and began to dream to advance to the fourth, fifth and sixth dimensions. Why isn't it a super cube? Maybe there is a super cube?

Sadly, after returning to the plane country, the square was regarded as a lunatic and was locked into the lunatic home. Unlike some of the animations and adaptations that are inspired by sugar, the uniqueness of this story is that it recognizes the danger brought by advocating social conventions. While arguing with other dimensions of square space, he is also defending the existence of other dimensions -he is a Kuer in a math.

At the end of the 19th and early 20th century, a large number of writers (Herbert George Wales, mathematician and science fiction writer Charlie Seton, he created the word "TESSERACT" for 4D cube), ) And the mysterious thinker (Peter Hispenski), explored the idea of ​​the fourth dimension and the significance of the fourth dimension to humanity.

Subsequently, in 1905, an unknown physicist named Albert Einstein published a paper that described the real world as a four -dimensional environment. In his "narrow sense theory", time was added to the three classic dimensions of space. In the mathematical form of relativity, these four dimensions are linked, and the word time and space enters our dictionary for the first time. And this combination is by no means casual. Einstein found that in this direction further inquiry, a powerful mathematical machine setting emerging from the response. It surpassed Newton's physics and can accurately predict the behavior of charged particles. Only by fitting the world into the four -dimensional model can electromagnetics be comprehensive and accurate. The theory of relativity is not only a literary game, especially when Einstein extend it from the "narrow sense" theory to the "broad sense" theory. Now, multi -dimensional space is full of profound physical significance.

In Newton's world map, the material is moved in time, especially under the influence of gravity. Space, time, material, and strength are different categories of reality. Through the theory of relativity, Einstein proves the unity of space and time, thereby reducing the basic physical category from four to three: space -time, material and power, and the general theory of relativity further incorporate the gravity into the space -time structure itself. From a 4D perspective, gravity is only a product of space shape.

To understand this unusual situation, let us temporarily imagine its two -dimensional simulation. Imagine a trampoline, a Descartes grid on its surface, and now put a bowling ball on the grid. The surface around the bowling ball will tease and deform, so the distance between some points and points will become farther, so that the inherent distance measurement in the space will be disturbed and become uneven. The general theory of relativity believes that this deformation is the impact of heavy objects such as the sun. Under this influence, the deviation between the actual space and Descartes and the ideal space of the Descartes leads to the gravity phenomenon we experience.

In Newton's physics, gravity appears out of thin air, and in Einstein's physics, gravity is naturally produced from the inherent geometry of the four -dimensional flow shape; Local, the strongest gravity, is sometimes called "rubber plate physics". The huge cosmic power enables the planet to run around the star, and the stars run around the galaxy. However, in Einstein Physics, this is just a side effect of space distorted, and gravity is actually geometric science in exercise.

If you enter the four -dimensional space to help explain the gravity, then think about whether there are certain scientific advantages in the five dimensions? Why don't you try it? A young Polish mathematician named Theodor Kaluza asked in 1919 that he believed that if Einstein could internalize gravitationalization into time and space, then another dimension could be used in another dimension. Interpret electromagnetic power as a product of higher time and space geometry. Therefore, Cruza added another dimension in Einstein equation, which made him happy that he found that in the five dimensions, both forces became the product of the geometric model.

You are like an ant running on a slender hose, never realized the dimension of the small circle under your feet

Although it can perfectly fit mathematically, the problem of additional dimensions is that it seems to have nothing to do with any specific physical properties. In a broad sense of relativity, the fourth dimension is time; in Caruza's theory, the fifth dimension is not anything that can be directed, seen or felt: it only exists in mathematics. Even Einstein hesitated to such a vibrant innovation. what is it? he asks. where is it?

In 1926, Swedish physicist Oskar Klein answered this question -a way that sounds like it sounds directly from the wonderland. Imagine, he said, you are an ant living on a long and thin hose. You can run back and forth along the hose, but you will not realize the small circular dimension under your feet. Ant physicist of ant microscope can see this tiny dimension. According to Klein, in the four -dimensional time and air we are, each point has a space circle like this, but it is too small, we can't see -it is many magnitude smaller than the atom, no wonder We will be missed so far. Only physicists with super particle accelerators have hope to see such a small scale.

Once the initial shock was overcome, physicists were quickly fascinated by Klein's thoughts. In the 1940s, this theory was elaborated in a mathematics and was applied to quantum conditions. Unfortunately, the scale with infinite new dimensions makes us unable to imagine how to verify it through experiments. In the calculation of Klein, the diameter of this small circle dimension is only 10 cm. In contrast, the diameter of the hydrogen atom is 10 cm, so the dimension we want to study is more than 20 ordered things smaller than the smallest atom. Even today, such a tiny scale is difficult to see. As a result, this idea is gradually no longer popular.

However, Caruza is not a person who is easily scared. He believed his fifth dimension and believed in the power of theory guidance, so he decided to perform his experiment. He chose to prove himself with the title of swimming. Caruza couldn't swim. After reading all the content of swimming theory, he felt that he had already mastered the water movement in principle. He was escorted by his family to the sea and devoted himself to the waves. You see, he can really swim. In Caruza's view, the swimming experiment supports the effectiveness of theory. Although he did not see the victory of the five -dimensional space he loved alive, in the 1960s, the idea of ​​Gaoxi Space once again attracted the attention of the theorists of the string theorists again. Essence In the 1960s, physicists discovered two other types of natural forces, both on the scale of sub -atoms. These two forces are called weak nuclear and strong nuclear force, which causes some types of radioactivity and gather quarks together to form protons and neutrons that make up the nucleus. In the late 1960s, as physicists began to explore the discipline of the strings (it assumes that particles are like small rubber bands vibrated in the space), Caruza and Klein's ideas have emerged to people's minds. Among the theorists, the theorists are gradually thinking about whether these two sub -atoms can also be described with time and space geometry.

It turns out that in order to cover these two forces, we must add another five dimensions to the mathematical description. There is no priority reason for the selection of this number. Similarly, these extra dimensions are not directly related to our sensory experience, and they only exist in mathematics. This has formed the hypothesis of ten dimensions of strings: there are four large -scale space -time dimensions (described by general relativity), and six additional "compact" dimensions (one for electromagnetic power, five for nuclear force for nuclear force ) All these dimensions are curled up in an extremely complicated and distorted geometric structure.

Physicists and mathematicians have spent a lot of energy to understand all possible shapes that may be presented in this miniature space and alternatives they may achieve in the real world. Technically, these forms are called Calabi-Yau Manifold, which can exist in any even higher dimension. The bizarre and complicated creation constitutes an abstract classification in a multi -dimensional space with extraordinary forms. Their 2D slices (the most direct visualization of their appearance) reminds the crystal structure of the virus. These fluids seem to have life.

Karabi-hill-shaped two-dimensional slice. Wikipedia

There are many versions of the theoretical equation describing 10 -dimensional space, but in the 1990s, Edward Witten, a mathematician from the Princeton High Research Institute (Einstein) Things may be simplified. He referred to his new theory as M theory and mysteriously refused to say what "M" represents. "M" is usually considered as a "film", but some people think that it is "matrix", "master", "mysterious" or "monster".

Our universe may be only one of many parallel universes. Each universe is an isolated four -dimensional bubble in the broad five -dimensional space.

OURS MIGHT Be Just One of Many Co-Existing Universes, Each A SEPARATE 4D BUBBLE IN A Wider Arena of 5D Space

So far, we have not collected any evidence that prove that these additional dimensions do exist -we still failed to reach the micro -landscape of the dream of swimming physicists -but the string theory has been proven to have a strong impact on mathematics itself. Recently, the theoretical version of the twenty -four dimensions reveals the unexpected connection between several major branches in mathematics, which means that even if the string theory cannot succeed in physics, it will be a rich pure theoretical insight. Source. Although the real world is unlikely to have 24 dimensions, in mathematics, 24 dimensional space itself is quite special: magical things can happen there, such as the sphere can be combined in a particularly elegant way. As for the world we love and existing, most string theorists think that 10 or 11 dimensions are enough.

String theory has another development worthy of attention. In 1999, Lisa Randall (the first theoretical physicist who obtained a lifelong faculty at Harvard University) and Raman Sundrum (an Indian American particle theorist) It is proposed that there may be an additional dimension in the cosmology scale described in the broadest theory. According to their "Brane" theory- "Brane" is the abbreviation of "film" -the universe we usually refer to may be embedded in a larger five -dimensional space, a super universe. In this super space, our universe may be only one of many parallel universes. Each of them is an independent four -dimensional bubble, located in a wider five -dimensional space.

The theory of Randel and Sandram is difficult to confirm, however, it is also regarded as the dawn of modern astronomy. In addition to themselves, Europeans could not imagine other physical "worlds", but now we know that billions of planets in the universe run around billions of stars. Who knows, maybe one day our descendants can find evidence about other billions of universes, and each universe has its own unique space -time equation. Understanding the achievement of spatial geometry is one of the milestones of science, but physicists may have reached the end of this road. Because of the facts, in a sense, Aristotle is right -the concept of expansion space does have logical problems. Although the relativity has achieved a lot of extraordinary success, we know that its description of space cannot be the final level because it cannot be established at the quantum level. In the past half a century, physicists have been trying to combine their understanding of space on the cosmic scale with what they observed on the quantum scale, but it has not succeeded. Integration requires new physics.

After developing a broad sense of relativity, Einstein's rest of his life is trying to "build all natural laws from the dynamics of space and time, simplify physics into pure geometry", just like the Princeton Higher Institute Institute Institute Institute Institute Institute "Robbert Dijkgraaf) said:" For him [Einstein], space -time is a natural cornerstone in the infinite scientific system. "Like Newton's world map, Einstein's world map can exist as existence as existence The main foundation and the stage of everything happened. However, in the tiny scale of quantum characteristics, the law of physics shows that the space we think in the past may not exist.

Some theoretical physicists are forming a view that space may actually be generated by some more basic substances, just like the macro attribute produced by the molecular movement. As Diqlav said: "The current view is that time and space is not the starting point, but the end point, it is a natural structure that emerges from complex quantum information."

Sean Carroll, a cosmologist at the California Institute of Technology, is one of the main advocates of the new space cognitive method. He recently proposed that the classic space is not "the most basic part of the real structure" and believes that we think we It is wrong to give it four or ten or eleven dimensions given this special position. Just like Dix Graff uses temperature to compare with temperature, Corol prompts us to be very similar to that of a large amount of water molecules. No separate water molecules can produce humidity. Only when they gather together can humidity become a nature. Therefore, he said that space is produced from more basic things at a quantum level.

Corol wrote that from the perspective of quantum, the universe "evolved in the field of mathematics with more than 10 dimensions" -it is a 10th place. It is difficult to imagine that this is almost impossible, and the total number of particles in the universe is compared with it. However, each dimension of this is a separate dimension in the mathematical space described by the quantum equation, and a new "freedom" that the universe can dominate.

Even Descartes may be shocked by the direction of his vision, and the dazzling complexity contained in the word "dimension".

Reprinted content only represents the author's point of view

Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences

If you need to reprint, please contact the original public account

Source: Hot Knowledge

Original title: "Fascinating" dimension

Edit: Paarthurnax

- END -