How to understand the independence of the event?

Author:Institute of Physics of the Ch Time:2022.06.26

Students will encounter a concept when learning the chapter of learning -the independence of random events. The explanation of the book is:

In intuitive, if the two random events Whether it does not affect each other, they think they are independent. At this time Immediately

< /g> < /g>

Here, " The probability that occurs at the same time is equivalent to the product of their respective probability "to define the event. "0" transform = "matrix (1 0 0-1 0)"> And events < g data-mml-node = "mi"/> (mutual) independent mathematical problem is no problem. However, how to understand " < /g> < /g> Does g> say this phrase? "? Today, Wu will talk to you about the independence of random events .1 Error understanding

When the concept of independence in the initial learning event, students often confuse each other, and they refer to the two random events < /g> < /g> It is impossible for two incidents to occur at the same time. From the perspective of the collection, that is, the two subsets do not intersect, that is, satisfaction

Use Waynetu as follows (where is the sample space:

The two events are mutually exclusive

Students often have some wrong "Lenovo" here:

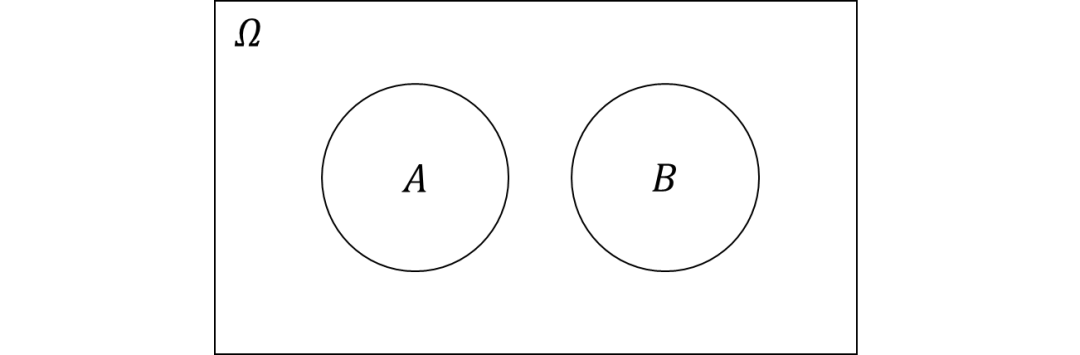
Independence stand No Yes off Lian < /g> < /g> In fact, the independence and mutual reprimand two concepts are confused.

We can give a simple example to explain the difference between the two.

For example, having a child, the existing two events :

Child Son is . Male

Child Son is . Women So obviously, at this time, the event is mutually exclusive. It is impossible for these two events to occur at the same time.

For another example, having two children, there are two incidents :

One Child Zi is . Male < /g >

two Child Zi is . Women Then at this time the incident is independent, because it is not difficult to understand: the gender and first child's gender and first The gender of the two children, the two must not affect each other, and the probability of gender is the probability of male or women is .

Now let's study the , which means "give birth to two children, the first child is a man, the second child is a female". ">The probability of is very intuitive, in fact::

< /g> < /g> Here, the definition of independence is actually calculated.

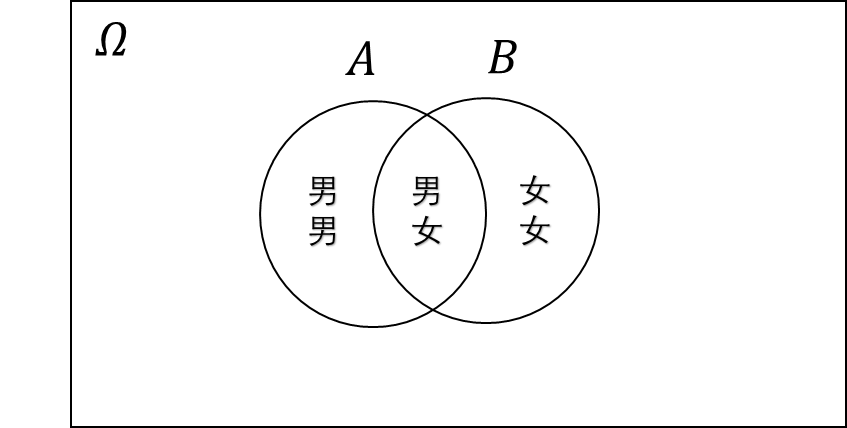
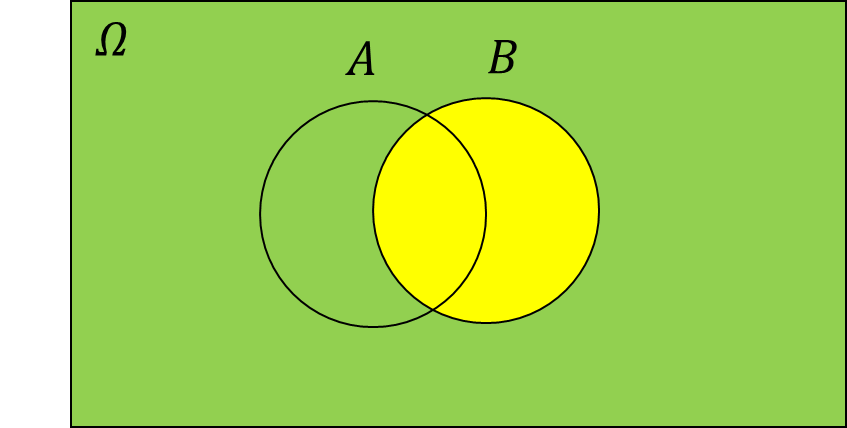
You can indicate the following in Wayne's map:

Two Event Independence

In fact, the incident also includes another situation (left): the first child and the second child are men. also includes another situation (right): the first child and the second child are women. (Of course, there are fourth type Case: The first child is a woman, and the second child is a man. This situation is also in the sample space , but it is In addition to two circles)

We found that although the incident The two are independent, but the two are intersecting. This is the most important point different from the mutually exclusive incident.

2 condition probability

So why does this phenomenon occur? To fully understand this, we must first learn a concept -conditional probability.

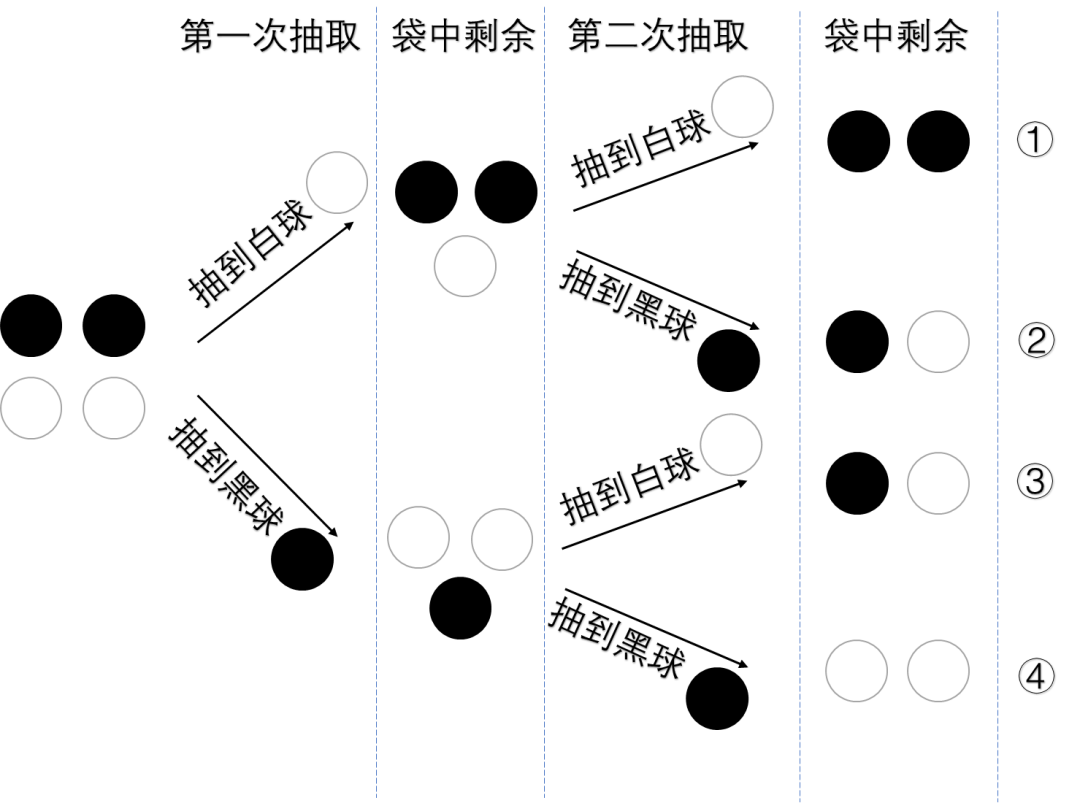
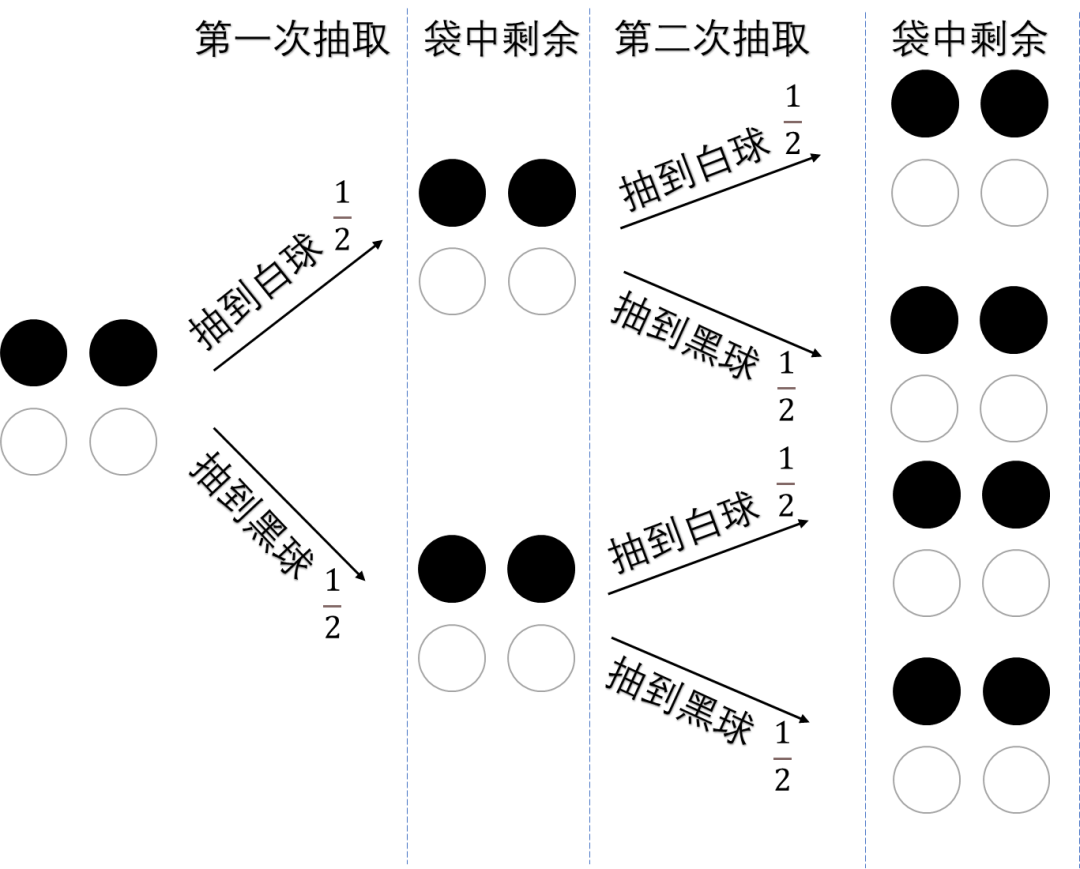
Now consider such a question: there are 2 white balls and 2 black balls in the bag. Now you do n’t put it back from the bag two times in a row.

This problem needs to pay attention to the condition of "not put back", that is, the first extraction will definitely affect the second extraction.

We can learn about this simple classification discussion:

According to the intention, what we want to happen is the path ①.

So, how to calculate the probability of path ①?

We remember the event < g data-mml-node = "mi" /> as::

One Times Pumping White ball

two times Pump to White ball Obviously, the probability of getting a white ball for the first time is

< /g>data-mml-node = "mo" transform = "translate (4830.3, 0)" />

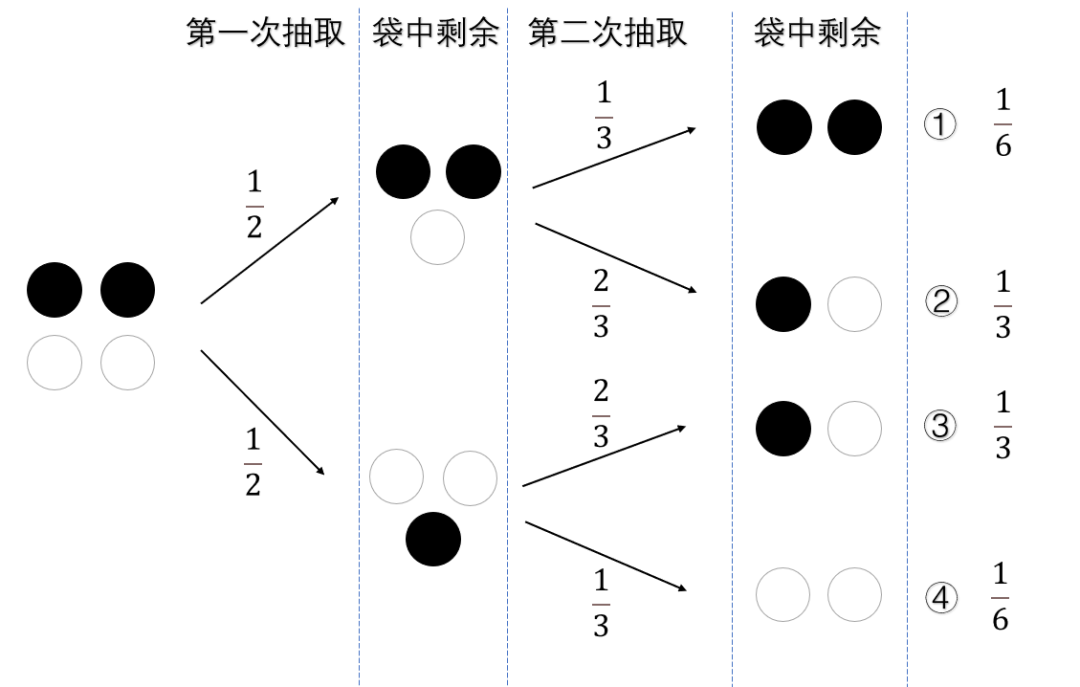
Next, we hope that when you get the white ball for the first time, the probability of the white ball for the second time, that is, " Under the conditions of < G DATA-MML-NODE = "Mi"/> The probability of occurring, we call it the condition probability, use It is expressed. Because After the bag occurs, the remaining remaining is" black, black, white ". , So

Then, the probability of the path ① (both twice draws the white ball) is

The probability can also be calculated in the same method. In fact, the sum of the probability of the total four situations is 1. 1.

3 How to understand the independence of the event?

After understanding the condition probability, we can understand what is the independence of the event.

In the above example, the event "Fill =" Currentcolor "Stroke-Width =" 0 "Transform =" Matrix (1 0 0-1 0) "> It has affected. And by the aforementioned discussion, The probability of the probability of the condition may be calculated at the conditional probability.

This reminds us of the formulas that the two events are independent of each other

< /g> In contrast, we can get one Conclusion: If < /g> Two If the incident is not independent, there must be

< /g> < /g>

In fact, in the example of white balls and black balls, < /g> Obviously not equal to , the root cause is that this problem is limited to "not put back" from the beginning The rules of the game. If the game rules are changed to "put back", the situation is completely different. Because the existence of this mechanism, the probability of each pump is constant, and it is always .

In other words, under the conditions of the placement, The two events do not affect each other, they are independent of each other. = "Currentcolor" Stroke-Width = "0" Transform = "Matrix (1 0 0-1 0)"> The two events are independent of each other, and there must be

In fact, this is the essence of each other's independent incident.

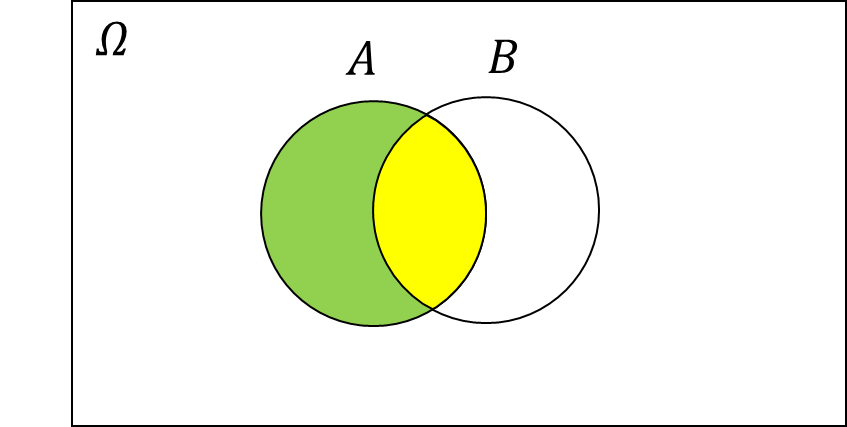
Understand from Waynetu, < /g> refers to In the sample space, . "stroke-width =" 0 "transform =" matrix (1 0 0-1 0) "> < /g> < /g> refers to /g> In ratio.

The two events are independent of each other. These two ratios are the same. Visible, for For example, is . Now you can understand what is what is Is the independence of the incident?

Reference [1] Jin Tianshou. Re-understanding of the independence of the event [J]. Mathematics report, 2012,51 (03): 24-26. [2] Malin. Comparison research, independent incident teaching effective measures [ J]. Mathematics report, 2008 (04): 55-56+58.

Reprinted content only represents the author's point of view