Why can't you feel the beauty of mathematics?
Author:Institute of Physics of the Ch Time:2022.09.19

Written article | Yuan Yaxiang
Almost all mathematicians believe that mathematics is beautiful. Students who have studied general letters know the famous Han-Banach theorem. The proposal of this theorem, Bamach, once said, "Mathematics is the most beautiful and powerful creation of humans."

Bamach (1892 ~ 1945)
The beauty of mathematics is reflected in many aspects, one of which is symmetrical beauty. Symmetry is a manifestation of the beauty of nature. In animal, plants and natural landscapes, the phenomenon of symmetry can be seen everywhere: beautiful butterflies, agile dragonflies, and peacocks on the screen are left and right; wide lotus leaves, fiery red red Many plant leaves such as maple leaves are also symmetrical; crystal snowflakes and horizontal rainbow are also symmetrical.

Symmetric examples in nature abound
Symmetric can be seen everywhere in mathematics. Aristotle, a well -known ancient Greek philosopher, once said: "Special performance, symmetry and restrictions of mathematics science, these are the highest forms of beauty."
Aristotle (about 384BC-322BC)
Many graphics in geometry are symmetrical, such as rectangular, round, and waist triangles on the plane, cube, cylindrical, and spheres in three -dimensional graphics. There is one or more symmetrical shafts on the plane, while the symmetrical stereo graphics have one or more symmetrical planes. Many of the collections studied in high -dimensional space are also symmetrical.
In real life, the straight line is one -dimensional, the plane is two -dimensional, and the three -dimensional is three -dimensional. If the time is considered, there is a four -dimensional space. In mathematics, you can consider any high -dimensional space. What's more interesting is that there are score -dimensional space. The division is a similar child set in the Eushi space, and its dimensions are usually not an integer. Most of the figures are very stunning, and some examples are given below.
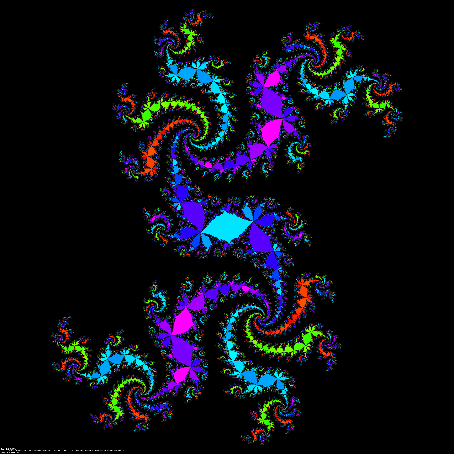

There are also a large number of symmetry in algebra. From elementary school A, B is equal to B multiplication A, to the symmetrical polynomial of middle school, and even the symmetrical matrix of the university, the symmetrical group, etc. are all symmetrical examples. Symmetry also provides ideas for many analysis techniques and proof methods in mathematics.

Symmetrical polynomial
When Aristotle talked about symmetry, the above also mentioned the order. "Preface" is an important concept in mathematics, and orderly things are harmonious and beautiful. German mathematician and philosopher Leibniz once said: "Sequence, symmetry, and harmony make us intoxicated ... God is pure and orderly, and he is the creator of the universe harmony."

Leibniz (1646-1716)
Leibniz and Newton independently established calculus, and now the mathematical symbols used in our calculus are derived from him. Leibniz's career is a lawyer, he invented and improved binary. It is said that this invention is closely related to China: According to legend, the French mathematician and missionary Bai Jin gave the Book of Book of Changes in China to Leibniz, which has inspired his invention binary.

Bai Jin (1662-1732)
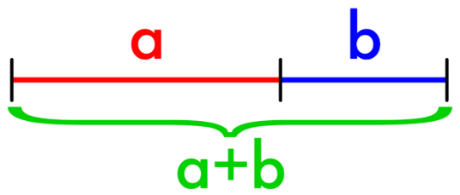
Another beauty of mathematics is the beauty of proportion. Professor of primary and secondary schools belongs to the Eushi geometry, and it is a systematic study of geometric properties in European -style space in ancient Greek mathematicians. Ou Jili has given a ratio called "middle -end ratio" in its "Geometry Original". Its definition is derived from: the points on one line segment divide it into two segments, so that the length and length of the long section and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length and the length of the paragraph and The ratio of the short section length is exactly equal to the ratio of the length of the entire line to the length of the length. This ratio is the so -called "middle -end ratio".

Eujiri (about 330-BC 275 BC) and "Geometry Original"
The line segment is divided into two short lengths, of which the length of the long section is A and the length of the short section is B. By solving a one -dollar secondary equation, you can find the middle and the middle of A/B (using the Greek letters φ as a mark). It is about 1.618.
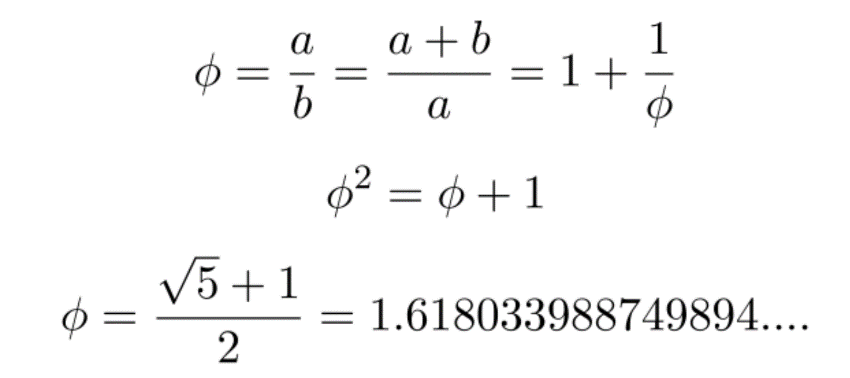
Many scientists highly respect the "middle -end ratio". German astronomer, physicist, and mathematician Kaifeller once said: "There are two major treasures in geometry: one is the Pythagoras theorem (Pythagorean theorem), and the other is the middle -end ratio. The former is comparable to gold. The latter can be called Baoyu ", which shows that he admires the proportion of" middle -end ratio ".

Capeler (1571-1630)
During the Renaissance, people liked to describe beautiful things as "glittering like gold". Therefore, this ratio was named "Golden Section" by German mathematician Martin Ohm. Readers need to remind readers here that Martin Om, a mathematician, is not a person in the physics unit in physics. The resistor unit was named after the physicist George Om, and Martin Om was George's brother.

Martin Om (1792-1872) and George Om (1789-1854)
Da Vinci, a scientist and painter in Italy, also likes the golden segmentation ratio very much. He has used the golden segmentation ratio in many places such as "Mona Lisa", "Last Dinner", and sketching "The Witrovie". According to Da Vinci, the beauty's belly button should be at the golden segmentation point of the entire height; similarly, the eyes should be located at the golden segmentation point of the head and so on.

Da Vinci (1452-1519 )'s masterpieces "Mona Lisa" and "Vitrowei"
The golden segmentation of the ancient Egyptian pyramids and the Paton Temple in Athens, Greece is also visible everywhere. Many animals and plants in nature are also reflected in the proportion of golden segmentation.

The relative position in the online segment of the golden segmentation point is the countdown to the end, which is equal to the sub -minus 1. We remember it as φ.
In the 1960s, Hua Luogeng, a well -known mathematician in my country, led the small team to promote preferred methods across the country, mainly to popularize the use of gold -dividing methods to optimize the method of optimizing the use of gold. This method is commonly known as the "0.618 method". Because of this, in our country, the golden segmentation ratio usually refers to 0.618 in the middle ratio. Simple beauty is also one of the beauty of mathematics. Many mathematical formulas are very simple. For example, Euler formula:

A short formula linked several of the most important quantities in mathematics: Euler constant E, virtual digital i, peripheral rate π, and 1 and 0.
Another concise and wonderful formula is Euler dot line formula. It depicts the inherent relationship of the vertex V, edge E and the number of surface fidium F: the number of vertices subtracts the edge number, and the sum of the number of surfaces is equal to 2.
Newton's Law F = MA is also a simple formula. It elaborates the basic movement law in classic mechanics. Its significance is that the force Fedes of the object F is equal to its quality m multiplied to accelerate A.

The examples of beautiful mathematics formulas in physics include Maxwell electromagnetic field equations (groups):
Maxwell (1831-1879) and its electromagnetic field equations (groups)
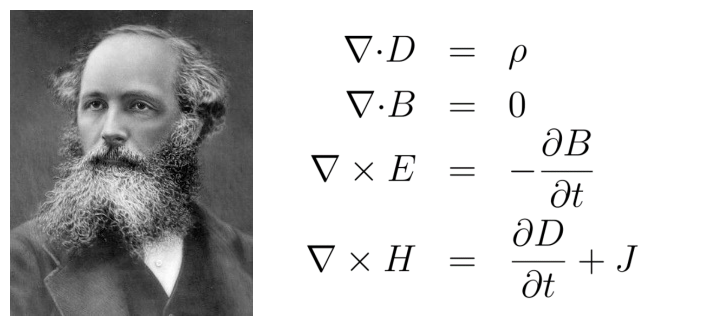
The simple four equations give the precise mathematics expression of electromagnetic field theory, showing the symmetrical beauty produced in the transformation of the electric field and the magnetic field.
The beauty of mathematics is also reflected in the wonderful number. Let's start with the hibirus theorem: Set the three edges of the right -angle triangle is 3, 4, 5, and the three squares of the three -side length of 3 plus 4 square meters equal to 5 square meters. Zhao Shuang, a Soochow mathematician in the late Eastern Han Dynasty to the Three Kingdoms period, clearly gave a description of the Pythagorean theorem in the "Zhou Calcontal Calculation Note": "Pythalums are multiplied by each other, and they are stringed. That's the string. "He also used the string map to give a proof of the Pythagorean theorem:" Press the string chart, and you can multiply the cymbals as Zhu Shili, and it is Zhu Shi Si. Zhonghuang Shi, plus difference, also become a string. "In 2002, the 24th International Mathematical Conference was held in Beijing.
"Zhou Ying Calcus" and the 2002 International Mathematical Conference meeting

Pythagorean theorem is called Pythagras theorem in the West because some people think that the theorem was discovered by ancient Greek philosophers and mathematicians Pydagras, and attributed the following proof to him. This proof surrounded the four triangles of the four crochemi strings into A, B, and C into a large square with a side length of A+B. The gap in the middle is a small square with a side length C. Using the large square area is equal to the relationship between small squares plus four triangular area, it can derive the pyrothebroken theorem. Note that the string chart is to surround the same four triangles into a square with a side length of C. The geometric methods of these two proofs of Pythagorean theorem are the same. In essence, one of them uses (A+B) 2, the other uses (A-B) 2 development formula.
Pythagoras (about 571BC-495BC) and the schematic diagram of its theorem
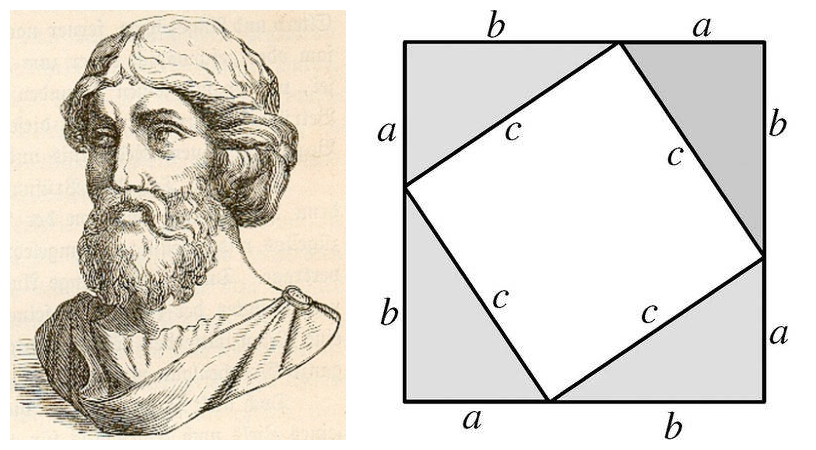
In fact, there is no evidence to certify Pythagras that have proved the Pythagorean theorem. But historical materials show that Pythagras obviously knows the Pythagorean theorem, and it is likely that he learns this wonderful conclusion from the Babylonians. Similar to (3, 4, 5), this array that can constitute three -sides of the right triangle is called Pythagoras. It can be proved that there are unlimited groups of Pydagras, such as (5, 12, 13), (9, 40, 41), (11, 60, 61), (13, 84, 85) and so on.
Cuba Babylon's proof of the Pythagorean theorem

Interestingly, if we replace the square in the Pythagin theorem into three squares, we can't find such an integer array to meet the laws. Ferma Dingli describes this conclusion: X's n -side side plus y's n, N -side N -do formula is equal to the n -side formula of Z, no positive integer solution is existed at when N is greater than 2. Ferma is a French amateur mathematician. He is a university in his university. At the age of 30, he served as a parliamentarian of Toulouse, and then served as a judge of the Toulouse Court. He often uses his spare time to study mathematical issues and communicate with Descartes (1596-1650) and Mason (1588-1648). Fema wrote the description of Ferma's theorem on the book's eyebrows in his collection of "Arithmetic", but did not give a certificate, but left a sentence: "I am convinced that I have found a wonderful kind of wonderfulness The proof, unfortunately the blank is too small here. " As everyone knows, the theorem behind this sentence proves that countless mathematicians have been thinking about it. It was not until 1994 three and a half years later that British mathematician Andrew Wiles gave a complete certificate.
Ferma (1601-1665) and "Arithmetic" (1621) (1621)

Another magical number theory is Gothic guess. Gota Bach was born in Cornisburg (now Russia, Russia), which is the place where the Euler seven bridge issues are located. Golbach has been a professor of mathematics and history at the Royal Academy of Sciences of St. Petersburg since the age of 35. Three years later, he went to Moscow as a personal teacher of Tsar. Since the age of 42, he has been working in the Russian Ministry of Foreign Affairs. It can be seen that he also uses his spare time to study mathematics.
In 1742, Gothic's letter to Euler proposed Gothic Bach conjecture: Any number of more than 2 can be written as three prime numbers (editor's note: also known as quality numbers, which can only be divided by 1 and itself). Because in the era of Gothic Bach, 1 was also a prime number, so Gothic Bachs guessed that in today's expression: Any even more than 2 can be written as two prime numbers. If "1" is used to represent a prime number, Gothic Bach guesses can be referred to as "1+1" for short. Although the description of this conjecture is simple, it is a world -class problem and is known as the pearl in the Crown of Mathematics. In the past 300 years, after the efforts of countless well -known mathematicians, it has not yet been completely proven. Gothbach (1690-1764)
In response to Goldbach's conjecture, several mathematicians in my country have made great contributions, including Wang Yuan, Pan Chengdong, and Chen Jingrun. It is particularly worth mentioning that Chen Jingrun proved "1+2" in 1966. This result is still the best progress in Goth's guessing problems. "1+2" refers to: All the sufficiently large number can be written as a content of a prime number and a product that does not exceed two prime numbers.

Chen Jingrun (1933-1996)
Clean and tidy is also an important factor in beauty. For example, if a person's face and body are dirty everywhere, no matter how long, everyone will not think how beautiful it is. The reason why mathematics is considered to be beautiful and has nothing to do with its neat beauty. As we all know, mathematics proves must be clean and can withstand scrutiny without any flaws.

John Locke, a British philosopher, doctor, and the father of liberalism, compares the solid, cleanness and indifference of mathematics to diamonds, showing his appreciation of mathematics proof. Locke has many famous theories, including "Human understanding theory" and "government theory". It can be said that his theory has inspired the American Revolution and the French Revolution, which has a great impact on the US Constitution and the Declaration of Independence. Such a well -known philosopher and thinker compare mathematics to diamonds, showing that mathematics is indeed beautiful.
Locke (1632-1704)
The beauty of mathematics is the ultimate beauty. This statement can be traced back to British mathematicians and logicist Russell. Russell is a well -known philosopher and writer who has won the Nobel Prize in Literature. Russell said that mathematics does not need to be modified and cold like sculpture. In his eyes, other arts, including dance and music, are not as beautiful as mathematics, and only sculptures can be comparable to mathematics.

Russell (1872-1970) and Michelangelo's sculpture "David"
In this place, readers may have doubts. Mathematics is so wonderful. Why do many people feel the same? In fact, the process and the ability to understand the beauty need to understand. As the so -called, the blind people will not think that the scenery in front of them is worthy of lingering, and the beautiful music will not set off the mood of deaf people. A person who does not eat spicy people from childhood cannot understand the delicious pepper in Hunan's population. Appreciation of mathematics is also a reason. If you have never entered the world of mathematics, understand and understand the incompetence of the numbers, graphics, and logic, how can you feel that it is wonderful?
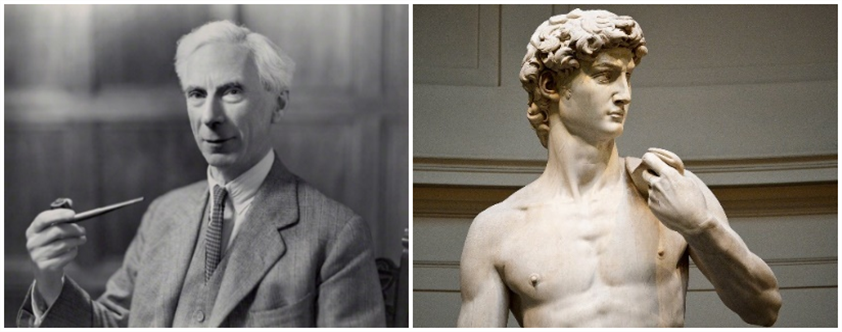
Editing Edit | livan
Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences
If you need to reprint, please contact the original public account
Source: Mr. Sai
Edit: Garrett

- END -
Beautiful!These elementary school students in Ningbo have wearing Hanfu to experience the charm of traditional cultural charm

Start at 7:30 tonight!The "Yan Zhao Shuang reduction in the Department of Education in the Hebei Provincial Education Department" came in the first session of Xiaosheng

At 19:30 tonight, how to help children walk well in the seventh lecture hosted by ...