Time crystal: a new material exploration

Shanghai Jiaotong University Cai Zi compiled from Pedram Roushan. Physics World, 2022, (4): 24

This article is selected from "Physics", No. 5, 2022

Because of its charming charm, the crystals have attracted our attention in the past few centuries. The well -known crystals, from snowflakes to diamonds, are usually composed of atoms or molecules arranged in space. Research on crystals helped us establish a set of frameworks that can be used to understand the orderly phase of other spaces, such as superconductors, LCDs and iron magnetic phases.

Periodic oscillation is another ubiquitous phenomenon. As small as atom, as large as the planet, it can appear in any size system. Over the years, we have used them to mark the passage of time, and it has even asked us to think about the possibility of permanent motivation. One of the common features of the cycle mode in space and time is that they all reduce the symmetry of the system: the periodic structure has obviously broken time or continuous translation symmetry in space.

In physics, space and time are usually closely related. Therefore, if a multi -particle system can show the periodicness of the space, it can naturally think of whether this cyclical mode can spontaneously appear at the time dimension. When the system of the system does not meet the symmetry of the system itself, it means that the system has a spontaneous symmetry. The most common example is the widespread crystals in nature. Its continuous translation of symmetry is broken, and replaced by the discrete symmetry in the space.

Space cycle and time cycle

In the past ten years, physicists have been thinking about whether the system of spontaneous time transition and symmetry can exist. The breaking of space translation of symmetry seems to be very different from the breakdown of time translation. Generally speaking, the system of space sequence is often composed of multiple interaction particles, and the system that presents cyclical oscillations in time usually has only a few degrees of freedom (Figure 1 (a)). In fact, it is difficult for us to find multiple examples of interactive particles oscillation together.

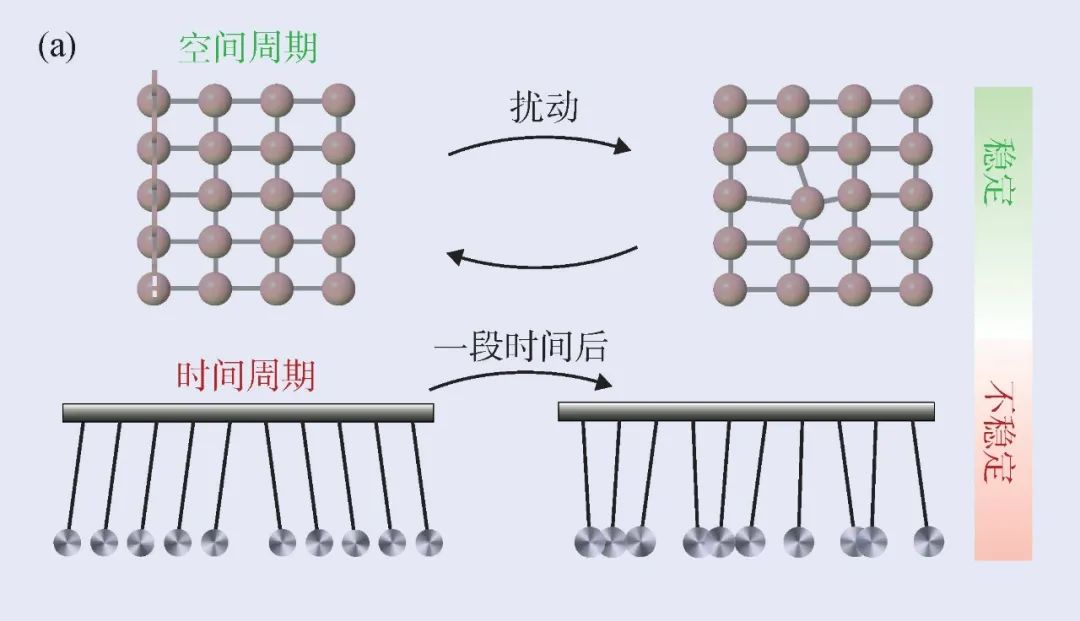
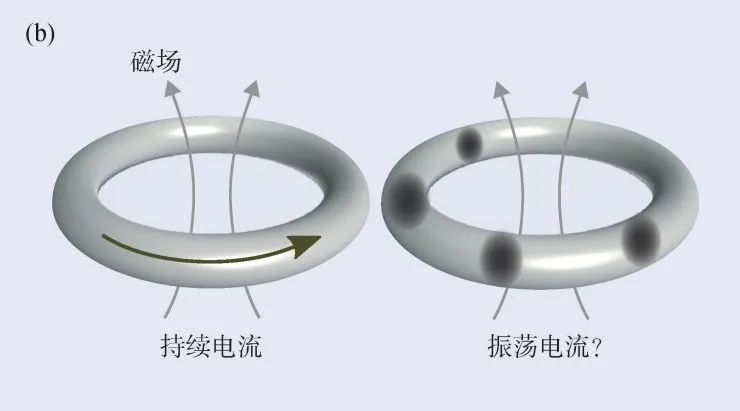
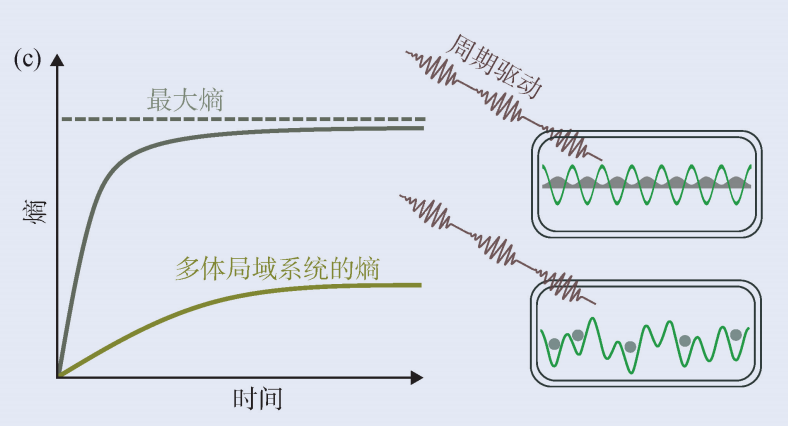
Figure 1 Time Crystal Challenge (A) Even if there are some disturbances, the spatial cycle sequence of the system composed of interactive particles is still stable, thereby forming the crystal phase we know. However, the time cycle sequence is usually stable for a system of one or more particles; (b) When the magnetic field passes through a superconducting ring, a continuous current will be generated in the ring. Verchek proposes that if the particles are interactive, a oscillating current may be generated, but the current that this oscillating current is proven to be unstable in the balanced state; The entropy of the size isolated system will not be reduced. Generally speaking, the driven system will absorb energy from the drive device to reach the state of the largest entropy. However, in the multi -body localized system, the entropy of the system will stabilize at a smaller value to allow the existence of time sequence

Is it possible to find a multi -body system that can continue to oscillate within an infinitely long period of time? Although collective synchronous oscillations can be observed in some multi -system systems, such as sound -vibrato or mass -point spring systems, these oscillations are generally unsustainable in isolated multi -body systems. Even if it can continue, it often needs to be highly adjusted to its initial configuration, and this high dependence on the initial state makes it unable to form a new thing.

The significant difference between the periodic periodic periodic periodic of multi -particle systems in the interaction is expected. After all, Einstein's theory of relativity has unified time and space into a whole. Although the time and space coordinates are linked through the Lorentz transformation, it does not mean the complete equivalent of time and space dimension, because there are still restrictions on causality.

Facing the second law of thermodynamics

For the forward, reverse evolution of time, or to choose any initial time for a given equation, the basic law of physics is invariant. But the second law of thermodynamics is an exception.

The second law of thermodynamics tells us that any isolated multi -body system will evolve spontaneously to its balanced state. Under this configuration, we cannot distinguish the passage of time by measurement of the local amount. The homogeneity that has time in time is contradictory with us wanting to build a stable time order (time -cyclical structure). This contradiction makes the research on time crystals very challenging.

In an open system, the system can exchange energy with the outside world, and the entropy theory of the closed system is no longer applicable. Therefore, we can build a stable time order by regulating the parameters of the system. However, in our definition, time crystals are a multi -body system of isolation interaction, which can oscillate in an infinitely long period of time. Therefore, the existence of a large amount of particle freedom in the system is the key to this definition.

For example, the oscillating observed in the superconductor Josephson does not constitute a time crystal. Although these oscillations can continue permanently, the degree of freedom of the entire superconductor is very limited: electrons that are paired at extremely low temperatures are binded together to form a cooper pair, and then form a macro -related state. Among them, the degree of freedom of different coasters is frozen, just like when we flip a coin, all of the atoms can only exercise together and cannot exercise independently.

Ten -year exploration

In 2012, the Nobel Prize winner Frank Wilchek first proposed a mechanism to achieve a permanent cycle oscillating. He suggested to pass a superconducting ring with a small magnetic field to generate a current of an indefinite cycle. However, although this spontaneous current is a permanent movement, it is not a permanent oscillation, because at each moment, the electronic density distribution on the ring is uniform and the same. Verchek proposed that the cycling curgot can introduce a weaker interaction to the cubic in which they can restrain them together. This will lead to an uneven distribution of particle density in the system of this system, and once the state of uneven space flows, this space will show a clear oscillation (Figure 1 (b)) Essence However, in 2014, physicist Watanabe Yuki and Oshichuan Zhengyi denied this conclusion by considering some implicit conditions that the system needed to meet. They further put forward the "unreachable theorem", which proves that systems with non -long -range interaction cannot form time crystals under their base state or thermodynamic balance.

Localization leads to stability

Therefore, in order to be able to get the time order steadily, it is inevitable to jump out of balanced restrictions. The easiest solution is to stay away from the balanced state by applying periodic pulse to the system. On the surface, the selection of the system of cycle -driven seems to be in violation of intuition, because such systems generally continue to absorb energy from the driver and evolve in the state of the largest entropy to destroy all the prefaces. However, recent studies have shown that if the system itself has a strong disorder, this disorderly can avoid energy exchange between different levels of system levels, thereby preventing the system's entropy from increasing. The system that meets this condition is called a multi -body localized system.

Due to the existence of entropy theory, most systems will eradicate the memory of initial information through energy exchange with the external environment, thereby reaching the thermodynamic balance. However, for a multi -body localized system, the disordered structure can make it unable to reach the thermodynamic balance, which can retain the memory of the initial information indefinitely. The entropy of the system is finally stable at a smaller value, so the presence of time sequences can be allowed.

Although there is a cycle driver, the net flow of energy becomes zero, and the stability of the entropy will be lower than its possible maximum value (Figure 1 (C)). Although the second law of thermodynamics requires that the entropy of an isolated system does not decrease over time, the saturation value of the entropy is lower than the maximum value it can reach and does not violate the law. The second law of thermodynamics only requires that the change rate of system entropy is not negative, and it can be zero or other positive values.

With the stability of the multi -body localized system

When a system is in a balanced state, it will no longer have a new energy flow with the surrounding environment and will not have new entropy. Many theoretical and experiments studies have shown that the localized localization system will also have these characteristics, but its essence is far from the balanced state. Therefore, it may be the only system that can generate a stable time crystal phase. So far, all known classic systems have no way to maintain an infinite time.

How stable is the localized localized system? Can we determine that they cannot reach the balanced state of maximum entropy? In fact, to date, whether the two -dimensional and three -dimensional multi -sample system system is still a controversial question. In 2006, researchers in the United States pointed out that one -dimensional multi -body localized systems can maintain their localized nature under any level of micro -disturbance. However, this does not exclude the situation of sub -stability, and it is likely that the system's thermal time is extremely long, and the characteristics of localization are displayed in a limited time. However, in 2016, George Parisi of the University of Virginia eliminated almost all non -micro -disturbance effects in certain systems, which made breakthroughs in the study of multi -body area.

Create a new thing

Even though we have observed the evidence of the time order, it is called a new thing that needs to meet certain specifications and requirements. We need to exclude the possibility of the current observed evidence is just a short -term behavior or just the possibility of accurately regulating the results within the range of minimal parameters. To achieve this, we will consider the following 4 factors to test the rigidity of time response: (1) In order to establish a non -balanced object, we need to consider the system under the limit of the system; (2) In thermodynamics, the phase can be accurately defined only under the limit of unlimited large size; (3) proves that a phase is stable to ensure that its standard mode is stable ; (4) It does not have dependence on the initial configuration.

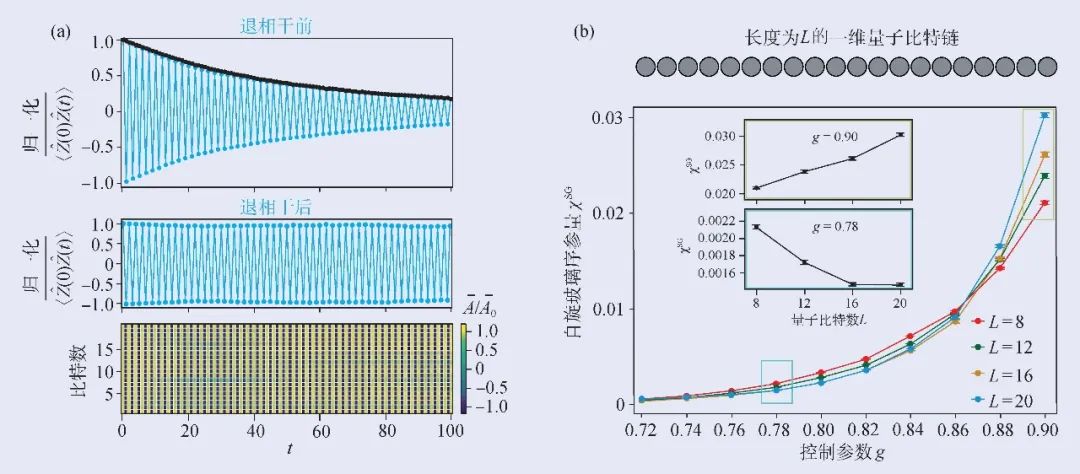
By using Google's "Suspension Suzuki" quantum processor, we realized the first convincing observation of time crystal phase on the noise medium -range quantum computer, and passed the above test standards. (i) In order to explore the infinitely long time response and prove that the observed oscillation is not short -lived, we designed a time reversal plan to distinguish the internal dynamics and the exterior rejuvenation (Figure 2 (a)). This enables us to observe a stable period sequence from a chain composed of 20 quantum bits. (ii) In order to prove that the observed oscillation can exist in a longer chain, we demonstrated the limited size marking, so as to determine the parameters of the phase change (Figure 2 (b)). (III) We also prove that this sequence can be observed within a large parameter range, and this system is indeed localized. Finally, (IV) we use the concept of "quantum typical" to indicate that there will be continuous oscillation for any initial state. Typical theory pointed out a pure state selected from the Hillbert space, the expectation value of the physical quantity of the pure state can be well consistent with the results obtained by the use of the average comprehensive department of statistics. Therefore, we can avoid the use of typicality to the index level of the sampling of the entire energy spectrum, and effectively determine the response of all the initial state.

Figure 2 By using the chain composed of 20 quantum bits, Google's quantum artificial intelligence team verified all requirements to achieve stable objects (A) After excluding the effect of retreating, they provided strong experimental evidence and confirmed to confirm that Observed a stable rather than a short -term existence, and this is also a signal of time crystal; (b) they tested the chain of different lengths and pointed out that the time crystal preface will increase with the size of the system before the phase changes increase. It becomes smaller and the opposite is opposite after the phase change point. The gradual verification of such things is never before in previous experiments.

Realize a dynamic phase

We realize a time crystal phase on the quantum processor in a unique way. Because all computing is usually implemented by a series of logical operations called quantum doors. This operation and the dynamics of the system itself are not connected. At the technical level, the expectation of Hamilton is not implemented on the processor. In this calculation, the use of quantum processors is roughly similar to that of classic computers.

However, this method of establishing dynamic phase is fundamentally different. The question is whether a stable phase can be produced from a multi -body isolation system containing a drive. For the exploration of such problems, quantum computers are a natural platform. However, this result still has some distance on the complete realization of dynamic phase: the response of judging the system under thermodynamic limit is still a huge challenge, because the coherent time of the system is limited. The core achievement of this work is to design an experimental method to provide the foundation for the next step.

As shown in this result, our development plan has general and established a scalable research method that can be used to study non -balanced objects on noise medium -range quantum computers.

Reprinted content only represents the author's point of view

Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences

If you need to reprint, please contact the original public account

Source: China Physical Society Journal Network

Edit: Lezi Superman

- END -