It is also unreasonable, it is not famous for π, but it is so important
Author:Institute of Physics of the Ch Time:2022.07.04
In the kingdom of mathematics, 5 numbers are very important. The content and role they contain far exceed the value itself. Therefore , I and e.
Like π, E is also an unreasonable number. Its value is e = 2.718281828459 ... infinite but not circulating.
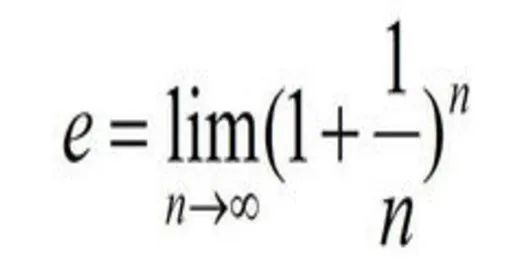
At the beginning, it occasionally appeared in the calculation results, but with the development of science, people gradually discovered that E is used in many uses, especially if it is used as a "bottom" to naturally, it can be simplified. Later, its application was even more widely used. It can be said that E is all -encompassing!
What really introduced e into mathematics was Swiss mathematician Jacob Bernubari.

Jacob Bernoulli
December 27, 1654 (this is the old calendar at birth, if the new calendar should be January 6, 1655) Jacob Bernubari was born in a businessman family in Basel, Switzerland.
In the history of science, Bernoulli, a family, can really be called scholars. Among the three generations of grandchildren, eight world -class famous mathematicians were released. Among these eight people, they also have physicists, astronomers and geographicists.
Their results include: pioneers of unlimited number computing, microconatory and differential equations, pioneers of statistical probability theory, and founders of the "Large Law". The proposal of the "San Petersburg Paradox", the founder of the fluid mechanics "Berunley theorem", and the famous scholars of curve research.
Since teenagers, Jacob has a strong interest in mathematics and astronomy. During the six years from 1676-1682, in order to learn the most advanced mathematics and science at the time, he studied throughout Europe and followed Robert Bosyr and Robert Hok, Christian Huyatus, Descartes and many other masters and many other masters. From learning, I read the papers and works of Frank Wanwamoto, Isaac Baro and John Valis.
In 1687, Jacobo served as a professor of mathematics at the University of Basel and worked here for life. In 1685, Jacob published a book of logic and probability. In 1687, another geometric science was published. In this book, he proved that any triangle can be divided into two vertical lines into an equal area. 4 pieces. In 1682 and 1704, Jacob published a total of five papers on unlimited research, and in 1689, he published the most important infinite number research results and large -scale theorem in statistics.
When studying unlimited levels in 1683, Jacob discussed an interesting "compound profit" problem, and even found e from the results!
The problem of compound interest is what people often encounter in daily life. For example, deposit in the bank's money, after expiration, the principal and additional interest becomes a new principal. "Interest", referred to as "compound profit" for short. Most people may think that in this way, the profit will be survived infinitely, and the profit will become higher and higher, so that it will reach endless.

Picture source: PEXLS
However, the situation is not the case. He wrote this problem as an unlimited level, which proved from it that if the number of money that was deposited at the beginning was 1, the number of deposits was infinitely large, and the sum of profitability tended to be a limited value, and this value was e! 1690 years Bernunley published this result in his series of papers.
On November 25, 1731, after many years, the big mathematician, Lyon Had Had Eric, talked about the number of E in a letter to mathematician Christian Gothbach and gave it a name. "Natural numbers", and take it as the "bottom" of the number of numbers, and have since there are natural pairs. The emergence of e public was in a papers published in the magazine of "Mechanics" in 1736. After that, E began to have its own position in mathematics and was quoted as a standard constant.
What surprised Jacob is that the strange number of E not only appeared in the "compound profit" calculated by him, but also repeatedly appeared in other infinite levels, such as ∑ (1/n), ∑ (1/n of the ∑ (1/n of the ∑ (1/n) 2) The number of levels of level; in addition, in the calculation of the probability, Jacob also found a countdown of an infinite level of sum of sum of sum of sum of sum of sum of sum of sum of sum of sum of sum of sum of sum of sum of sum. The E -value appeared again.
The problem of "hat storage" was a topic that was interested in the mathematics industry at that time. Due to the introduction of the E value, Jacob finally calculated it. This question is very interesting. It is said that many guests are invited to participate in a party. Before entering the house, everyone must hand over the hat to the gatekeeper, and he puts the hat into their own boxes. Originally, the guest's name was marked on each box. The hat should be seated, but the doorman did not know these guests. When he put the hat, he was freely put in the box. Essence

Picture source: PEXLS
Therefore, the problem appeared. When taking the hat, how many times do all the guests need to choose at most to find their hats? Of course, the first person to take a hat is the most difficult. This is also a question of levels. When the number of guests tends to be infinitely large, E is shocked in the calculation results of Jacob. Then, in the calculation of the standard normal distribution, he found the E value again. In the later period of Jacob's mathematics research, he liked to study various curves, including parabolic lines, dual curves and spiral lines. When studying the dual curve function y = 1/x, when the area contained in the calculation curve, it meets the E value. Later, Jacob studied the spiral line and met again with E. There are 5 forms of spiral lines, which are the most common in nature in the natural world. When studying the number of spiral lines, Jacob discovered a very interesting phenomenon. The close line of the digital spiral line was also a number of spiral lines. Line, in a spiral structure, contains multiple layers of spiral structures. This wonderful feature makes him amazed!
It is also loved by the artists. The well -known British painter and art theorist Tauzz once deeply felt that the spiral shape that gradually contracted to the center had its incompetent beauty!
The spiral line often appears in the murals that are left in the famous paintings or the ancestors left. They represent the ancestors' imagination of the entire universe, and they also declare their feelings in their hearts. The favor of the line has its internal mathematical reasons.
In biology, the structure of the conch shell, the sorting of sunflower seeds, human fingerprints and hair rotations all show the characteristics of spiral.
The structure of the conch shell

As the protein of the basic material of life phenomena, its function is so efficient during the entire process of participating in the life of the life, and its mystery is also related to its spiral structure. The protein's polypeptide chain is spiral, which determines the genetic substance -the nucleic acid structure is also spiral, and the mysteries in these spiral structures are all left and right by E.
E also appears in physics, and E. The second law of thermodynamics that unknowingly controls the destiny of nature has E; in nature, from the airflow of spiral nebula and spiral galaxy, typhoon hurricane, to a ray of green smoke, Rising, the eagle soaring in the air, there are E existence; when a piece of music sounds beautiful, you can find E by carefully studying, you can also find E from the rhythm; music is spoiled, and the air vibration generated by "music" is also a kind of Spiral end; even after a long years of evolution, the structure of the ear in the hearing organs is spiral.
Typhoon Hurricane's airflow

It seems that E is omnipresent. E always E in the core of human beings play a role. Although the place where the place is different, the same way is hooked with this natural number E.
In 1690, when Jacob introduced E, his estimation value to E was only first after the decimal point; by 1748, when Euler used this value, it had accurately reached the 23rd after the decimal point; 1949 1949; 1949; 1949; In the year, American physicist John von Normanman used a computer to calculate E to the 2010 position after the decimal point; by July 5, 2010, E showed a clearer appearance to the world and reached the decimal point. The latter 1 000 000 000 bits! One thing to be sure, no matter how hard it goes through, human beings cannot see its "true value". It seems that one of the internal reasons is that the reason why nature cannot fully show its true appearance is contained in the unreasonable number like nature E and π. This is the mystery of nature!
In Jacob's life, his most beloved is the screw line. He believes that this is the most magical and most desirable mysterious line. The confession states his wish: "I will come out of the same style."
Jacob's tombstone

Jacob's "soul" accompanied by E, hidden in the spiral spiral he loved!
Source: "365 days in the history of science", slightly deleted
Author: Wei Fengwenwu Yi
Part of the source network
Copyright belongs to the original author
Edit: Zhang Runxin
Reprinted content only represents the author's point of view

Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences
If you need to reprint, please contact the original public account
Source: Original Reading
Edit: Just_iu

- END -
Deep development in Dashan, Qin Feng Chuyun dialect -Rural Revitalizing Academician Activities Expert Group to Laosi

With more than 4,000 years of history, the ancient city of Shangjin ushered in a n...
Huawei response: have nothing to do with Professor Chen Chunhua
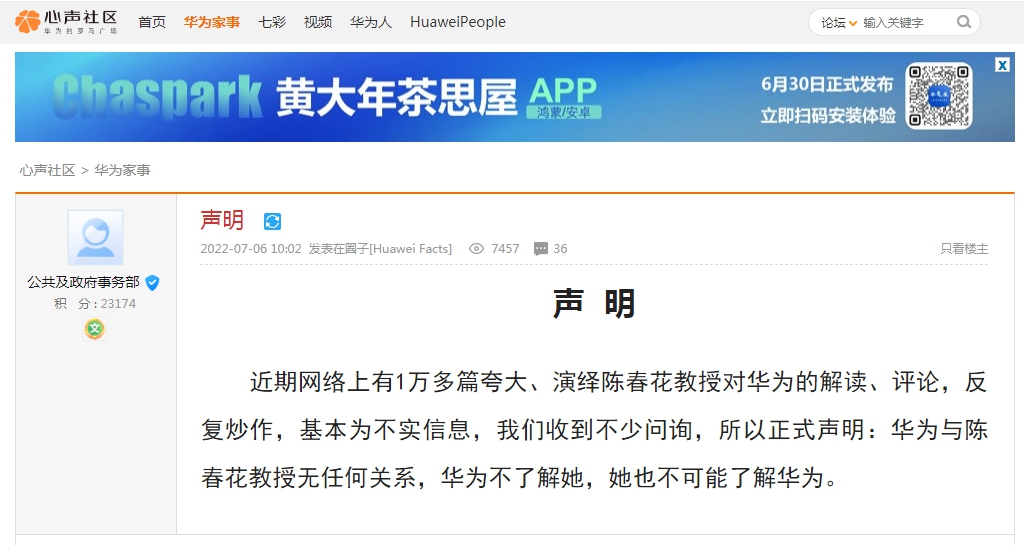
Zhongxin Jingwei, July 6th. On the 6th, the Ministry of Public and Government Affa...