Talking about calculating condensate physics

| Author: Meng Jingyao Ma Tianxing Lin Haiqing

(1 Department of Physics at Beijing Normal University)

(2 School of Physics, Zhejiang University)

(3 Beijing Computing Science Research Center)

This article is selected from "Physics" No. 9, 2022

Abstract Calculation Physics Taking Computer as a tool, calculating methods and calculating software as a means, in recent years, it has developed rapidly in recent years. In terms of studying material structure and physical laws, a large number of traditional physical problems have been solved. Experimental triple strength. The article briefly introduces the origin and development of calculating physics, focuses on the application of calculating physics in condensed physics, and introduces methods including accurate diagonal, numerical reconciliation group, Monte Carlo, dynamic average field and other methods, and also Elapse the characteristics of each method. In the two aspects of exploring the novel physical phenomena and development calculations, the future development direction of calculating condensate physics is discussed.

Keyword density generalization theory, accurate diagonalization, re -righteousness group, Monte Carlo, dynamic average field

01

introduction

As one of the fastest -growing areas in the past 20 years, computing physics uses computer as a tool, computing methods and calculation software as a means to study and discover the laws of material structure and its movement. It has become a second -level discipline that is equally important and sustainable as experimental physics and theoretical physics. Initially, physicists used early computer to study the state of state and non -linear dynamic problems of the substance composed of a single molecule of interaction, and calculated that physics came into being. In the 1950s, a numerical simulation represented by Monte Carlo solved a large number of statistical physics and related problems. In the mid -1970s, Wilson proposed the numerical re -righteous group method to solve the problem of near vine in physics. At the same time, the theory of density general letters has also developed rapidly. It is widely used to study the electronic structure of various materials, explain the results of experimental measurement, and successfully predict the basic characteristics of some materials. Since development, the scope of calculating physics research has continued to expand, and from basic physical phenomena to the fields of material science, chemistry, information, life and other fields, has become a difficult problem for solving traditional physics research paradigms, reducing experimental costs, and even alternative experiments, revealing new new which shows new experiments, revealing new new which shows new experiments, revealing new new which shows new experiments. The necessary means of physical laws and effects.

The condensation state system is a quantum system that is formed by a large number of electrons and atomic nuclei. Setting state physics is one of the fastest -developed disciplines in physics research over the past 40 years. Through the continuous improvement and development of high -performance computing of modeling, computing physics has established a bridge of theory and experiments, micro and macro, and provides a new and effective scientific research method for the condensing state. Calculate the condensate physics for the condensation system mainly based on solid materials, to study the spatial structure of the atomic atom, the coupling of the atom and electronic charge, spin, and rail freedom, and various quantum states emerging from this, and develop and develop. The corresponding calculation method. Starting from quantum mechanics, calculating condensate -state physics design and determine the material system with different functions, structures and components at the atomic level, and calculate the structure of the electronic energy of the material and its interaction with the lattice. Basic characteristics of materials. On this basis, study the strong connection between the multi -electronic interaction system, find various derivative quantum phenomena caused by different competitive factors, and display the physical effects produced by the system under the control of the outside of electrical, light, magnetic, etc. Many physical mechanisms.

In the past 40 years, the discovery of a large number of quantum phenomena, including quantitative Hall effect, high temperature superconductors of copper oxide, iron -based superconductors, pomosciences, heavy -fames, quantum critical crimes, etc., which enriches the research connotation of condensed physical physics. , Promote the rapid development of multi -body quantum theory. Many new phenomena are derived from the coexistence and competition between micro -freedoms such as electronic charge, spin, orbit, and lattice in the system. They usually appear in low -dimensional systems. Its common feature is the Kulun interaction between electronics and quantum rising quantum rising. The fall is strong and cannot be explained by the existing solid theoretical framework. When these freedoms are strong, traditional research methods are not applicable, and strong correlation electronics can not be described by the theory of symmetrical deficiency in Landau -Ginzburg -Wilson through the Langdon Fermi liquid theory. If you want to solve these problems, you must develop new theory and calculation methods.

Starting from the definition of some basic interaction models on the grid point, scientific researchers have studied the physical properties of the quantum multi -system system. The proposed models include the Hubbard model, T -J model, Fermiko -self -rotation coupling model, Heisenberg model, etc. Various types of strong corporation models have received widespread attention and have achieved important results. For example, although the Hubbard model greatly simplifies the electronic -electron interaction in solids, it can still describe a variety of physical phenomena, including metal -insulators transformation, magnetic sequence transformation, stripes and superconducting symmetry. After a series of development after the discovery of high -temperature superconductors, the research of the Hubbard model has richer connotation, such as the Anderson -Hubbard model, the HOLSTEIN -Hubbard model, etc., including disorderly, electro -sound interaction and other factors, providing us with more more interaction. Broad application prospects. Similarly, the research of the Heisenberg model helps people deeply understand the novel physics in the quantum spin system, such as the anti -iron magnetic base state in the cage system, or the use of the quantum Monte Carlo method to study the spinning bolic toast. It is worth noting that there is no universal method to solve these statistical models or quantum poly body models. The following four methods are: precise diagonalization; numerical weights, including WILSON numerical weights, density groups, density, density, density, density, density, density, density, density, density, density, density, density, density, density groups, density, The matrix heavy righteousness group, tensor of heavy righteousness groups, etc.; Quantum Monte Carlo simulation; dynamic average field method. For different systems and different research objects, scientific researchers usually use appropriate calculation methods to solve specific problems. The remaining parts of this article are arranged as follows: Section 2, briefly calculate the connotation and history of condensation physics; Section 3, introduce the main models and methods of calculating the field of cricket state physics; section 4, briefly explore recent research progress in related fields With the direction of development. 02

Computing physics: connotation and history

Calculating physics is a discipline that is aimed at a given physical system, combining numerical algorithms and computer programming technology, and studying material structure and laws. Simply put, computing physics is to use advanced computing power to solve complex physical problems through numerical calculations or simulation. In the real system, the efficiency and scope of research are affected by many real world factors that are difficult to change effectively; and because of the convenient setting of environmental parameters, calculating physics provides the possibility of deep understanding of system physics. In the process of trying many solutions, calculating physics helps to discover new physical phenomena, explore new physical effects, solve or interpret physical problems in the project according to the known laws of physics; The physical system that is difficult to study by extreme conditions and other methods is used for numerical simulation. Calculating physics can help us discover new physical laws and expand the cognition of the material world.

Computing physics originated in the Manhattan plan during World War II. Researchers usually use calculated physics for simulation when solving the problem solving the problem and needing too much data. In my country, computing physics began in the 1950s and originated from major needs in the national security field, especially the traction of the "two bombs and one star" task. Physicists use early electronic computers to study numerical points, micro -division equations, material state equations, and non -linear dynamics issues to present every movement of the micro -world in front of people. In the initial stage of development, calculating physics is mainly used as auxiliary tools for theoretical physics to solve the complex computing problems encountered in theoretical or experimental physics research; Essence Generally, only by calculating the physical characteristics of the relevant materials can be considered that the given phenomenon or material characteristics can be considered fully understood.

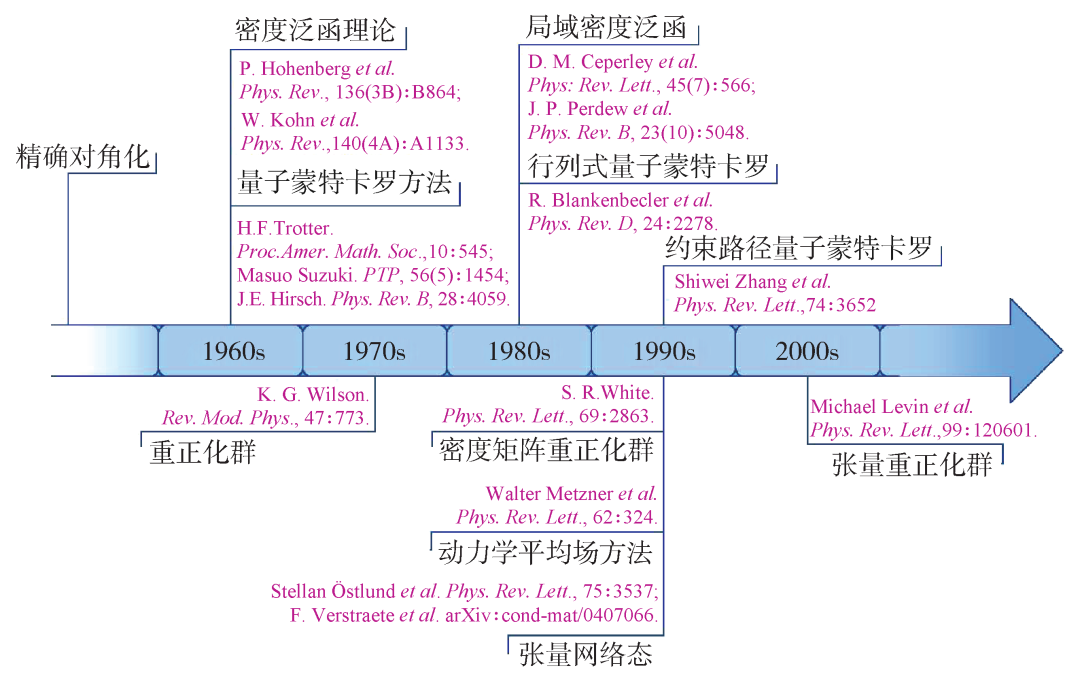
Since the first computer was invented in the 1940s, the computer performance has developed rapidly in accordance with Moore's laws doubled every 18 months. In 1982, Wilson won the Nobel Prize in Physics with the Numerous Headsmate Group, announcing that computer assistance to solve the time of complex physical problems. In the late 1980s, under the organization of Mr. Li Zhengdao, research institutions such as Columbia University and other research institutions jointly promoted and developed parallel computers to promote the development of high -performance computing technology and theory. The development of computers enhances computing capabilities and also prompted computing physics to solve numerical problems in various fields, such as biophysics, celestial physics, chemistry, and material science. Recently, with the gradual slowdown of the performance of single -core processors, parallel processing has become a representative of high -performance calculations. As shown in Figure 1, the proposal and improvement of a series of important calculation methods has spawned the emergence of a large number of important scientific research results and demonstrated the vigorous development of calculation physics. Today, due to the high computing power and high storage bandwidth of the device, and the availability of standard programming languages ​​and tools, graphic processing units (GPUs) have become a large -scale parallel computing option. The use of multiple GPUs can shorten the problem to solve the time and improve the accuracy of discreteness, and this is exactly what the calculation of condensate physics research needs.

Figure 1 Calculate some important methods and representative articles in the field of physics. The development and improvement of the method helped us deepen the understanding of various systems' physical nature

As one of the fastest development disciplines, calculating physics also provides a reliable research method, even the only means for many subjects limited by practical conditions. On the one hand, for complex physical systems, such as quantum multi -body interaction systems, although the theoretical framework of the system has been developed, it is almost impossible It's very difficult. On the other hand, for some extreme conditions in reality, such as ultra -high pressure above 500 GPA, extremely low temperatures under 1 mk in solid systems, and a stable constant strong magnetic field above 50 t, it is still difficult or even unlikely to carry out actual actual situation. Experimental research. Calculating physics can provide appropriate solutions for the above situation, and has become an important physics discipline that is important as experimental physics and theoretical physics. It is also an important pillar of supporting physics and its interdisciplinary development. In terms of scale, people engaged in computing physics research have exceeded the number of people engaged in theoretical physics research. The computing simulation expands the depth and breadth of physics research, shorten the research cycle, reduces the cost of research, and accelerates the research process. There are great differences in the research content and methods of calculating physics for different standards. Therefore, to conduct research, first of all, we must first establish a basic physical model based on the research objects. Based on this, develop an effective calculation method, and then find the solution to find problems through large -scale numerical calculations and simulation. The study of the calculation method includes two parts: first, the core algorithm of the use of physical or calculating mathematics to establish a solution problem; the other is to establish corresponding calculation software and databases according to physical objects and algorithms. Algorithms are the core of research and the key to determining the simulation efficiency and reliability.

As a discipline that can change traditional physics research paradigms, the scope and data processing efficiency of calculating physics is greatly improved as the machine computing capacity is continuously enhanced and the algorithm is continuously optimized. With the popularization and development of the informatization era, computational physics has been widely recognized due to its controllable research costs, repeated results, and practicality. By effectively shielding the impact of the main factors, computing research can study the physical characteristics of complex systems from theoretical height, explore the core or key scientific factors in the actual system, and improve the effectiveness and timeliness of cutting -edge exploration. At the same time, it can also predict new physical phenomena, physical effects, physical laws, and new materials to achieve real -time control and analysis of complex data, real -time control and analysis of experiments. As research gradually focuses on non -linear problems, random environment and non -parsing solutions, calculating physics can also solve problems that traditional analysis research cannot solve according to the existing theoretical framework or model. In addition, some new theories usually have no appropriate experimental system for inspection in the early days of establishment. Calculating physics can help reveal the new physical effects and laws; or assist researchers to explore new material properties and obtain measurement accuracy higher than the experiment.

03

Quantum multi -body computing: Calculate the model and method of condensation of state physics

3.1 Precision Delivery

At present, accurate diagonal is a relatively mature computing -centered physical method, and it is an important tool for studying the physical nature of the quantum multi -system system. It can not only provide a benchmark for approximate theoretical calculations and quantum Monte Carlo methods, but also helps to deeply understand the subtle features that cannot solve multi -body problems in thermodynamic limits. For a limited quantum system, Hamiton can always be represented by a matrix. The accurate diagonal method solves the standard of the matrix and the vector of this sign, and calculates the physical properties of the system through the lowest standard values ​​and this vector to calculate the various base state expectations and related functions. The advantage of this method is that there is no need to do any approximation. The disadvantage is that the system size that can be processed is small, or the number of particles is small. This is due to the total number of system freedoms, that is, the number of matrix dimensions of the Hamilton volume increases the index with the increase of the system size. This problem is also called the "index wall problem". Of course, this limitation may also be surface limitations. For example, in the one -dimensional system, the length is less than that of the lattice, and the use of this method can also obtain representative physical results. The accurate diagonal algorithm of limited temperature is also applied to the dynamics or limited temperature thermodynamics of research models. Through the combination of Monte Carlo method and dynamic average field, the theoretical depth that accurate diagonal methods can be involved have been expanded.

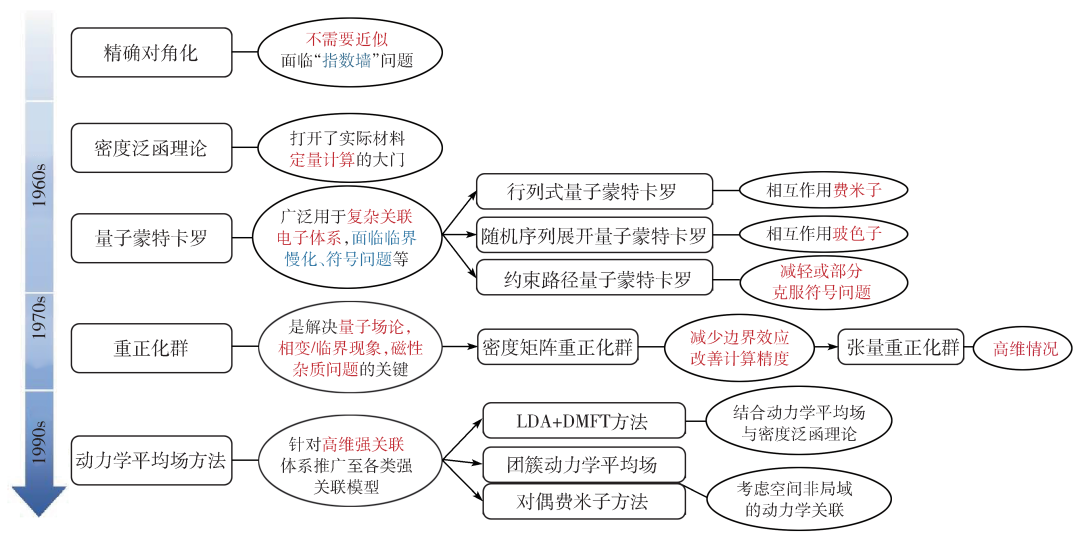
Other mature research methods include Wilson numerical re -righteous group and density matrix heavy righteousness group. And a series of methods including quantum Monte Carlo, Zhang Mengzheng Group, and dynamic average field, although it has undergone a certain degree of development as shown in Figure 2, it is relatively not perfect, and it still needs to be further improved.

Figure 2 Calculate the development of some important methods in the field of physics. The characteristics of the corresponding method of the left side are described in the oval box

3.2 Density Grand Letter Theory

Before the 1960s, similar methods/theories were generally used, such as Hartree's approximation to calculate the electronic structure of the condensed state system. Although these methods have certain limitations, they still provide tools for related research. In the 1960s, Kohn and its collaborators proposed the theory of density general letters (DFT) and established the Kohn -SHAM equation. Combined with the approximately similar letter of local density, it laid the foundation for the calculation of contemporary electronic structure. For this reason, Kohn and the founder of computing chemistry Pople shared the 1998 Nobel Prize in Chemistry. In the 1980s, the advancement of the quantum Monte Carlo method promoted the development of density general letter theory. A series of local density letters that are suitable for different electronic density and improved calculation accuracy came into being. With the continuous development of the theory of density and generalization, calculating methods and computer performance advances, calculating condensed physics has gradually interpreted the experimental data qualitatively, turning to quantitatively predicting the materialized properties in the actual material. The development of density general letter theory leads the study of electronic structure and is regarded as a major breakthrough in calculating condensed physics. In many fields, such as nuclear physics, molecular physics, chemistry, etc., they have been valued and widely used. In fact, the theory of density general letters not only affects multiple disciplines, but also has also received feedback from various research areas. For a long time in the development of density general letters, due to its dependence on the average field in specific applications, the physics community lacks sufficient attention to density general letters. In the early 1980s, with the establishment of the parameterization of associated with the exchanges under the approximate of the local density and the development of a broad gradient, people began to use a large number of density general letters theory to describe chemical reactions. While promoting the development of theoretical chemistry, density letters have gradually become an important method in calculating condensed physics.

3.3 Monte Carlo method

The root cause of the quantum Monte Carlo algorithm dates back to the 1950s, when ULAM and Von Neumann proposed an idea to calculate the function of the matrix through random methods (that is, random walking in matrix space). In 1962, the idea was first applied to physical problems by Kalos and others. In 1973, KALOS et al. Reported the application of this concept on multi -body issues for the first time. In 1977, Suzuki and others completed the simulation of the quantum spin system. Since then, the method of quantum Monte Carlo has ushered in rapid development. Its main idea is to simulate the probability of practical processes on the computer, and then statistically deal with it. The key point of this method is random. The early Monte Carlo method mainly used Suzuki -Trotter to decompose the dimensions of the dimension separately to calculate its distribution function to study the quantum magnetic model; use the Metropolis algorithm in the phase space to effectively sample to meet the meticulous balance. As the algorithm is updated slowly, the group update algorithms such as Wolfff are gradually proposed. Usually, on the basis of path integrals, a D -dimensional quantum system is equivalent to a D+1 -dimensional classic system, so calculating the score function of the quantum polymorph model can also be implemented by Monte Carlo simulation.

Today, the quantum Monte Carlo method is widely used. In the early 1980s, BlankenBecler and others proposed a ranked quantum Monte Carlo algorithm to study the Fermi subsystem in the interaction; in recent years, this method has also been used to study Fermi noodles or Dirac Femumo and the critical Boson field. Coupling problem. For interactive bosom infrastructure and spin system, the HandScomb method developed in 1962 is suitable for the self -spin 1/2 Heisenberg model with nearest neighboring interaction to avoid the inherent system errors in the path integral. In addition, Monte Carlo combines the principle of Monte Carlo points and base state for calculating the expectations of the expectations of electronic Hamilton to introduce the idea of ​​"important sampling". The restraint path of the quantum Montecaro method, by converting the base state from the projection of the initial state to the important sampling branch in the SLATER ranked space, the path of random travel and restraining the random walking path. The symbolic problems can Simply solve the method of the Fermiko system.

3.4 Numerical heavy righteousness group

In the early 1970s, Wilson introduced the basic concepts of heavy righteousness groups and the numerical re -righteousness group named after his name. In Wilson's formula, the short -range and high -energy rise and fall are gradually integrated to obtain effective descriptions of long -range and low energy. The method of heavy righteousness provides researchers with practical tools for studying the association/rising system, and the conceptual understanding of basic interactions in the secondary phase changes and high -energy physics, and the point charge in quantum electrodynamics in quantum electrodynamics The problem of divergence and the gradual freedom of quantum dynamics plays a key role. In 1992, White proposed the method of density matrix heavy positive group method, using the characteristics of the intensive density matrix. The locality of the Hillbert space was reduced in the real space. Can effectively solve the polyphonic function. Nowadays, the density matrix heavy righteousness group has become the most accurate and systematic method for studying the one -dimensional short -range association system. It has given the result of close solution in Hubbard, Heisenberg and other models. In addition, the close connection between the density matrix heavy orthodox method and the theory of quantum information began to force the calculation of complex quantum information theory, and it can be applied in a more concentrated way through new views of its internal principles. In this sense, the density and normalization method will be at the forefront of increasing entanglement between condensed physical physics and quantum computing. The density matrix heavy righteousness group mainly processes the low -dimensional and strong Hamilton volume, and when the number of dimensions of the system exceeds one dimension, because the entanglement entanglement increases with the size of the system size, the required computing resources will also increase with the system size index. The application range of this method has been greatly limited. One of the ways to solve this problem is to develop the method of re -righteousness in a network state, and it is also referred to as the method of tensoring and positiveization. In 2007, Levin and NAVE used the idea of ​​quantum information theory to develop the method of weight and positive groups, which can effectively solve the two -dimensional classic lattice model, which can be exempted from symbolic issues and applied to models with complex weights. Since then, various methods based on the principle of change, including the optimization of the change of the base state and the "full update" method of the determination of the domain tension, have also been developed to further improve the calculation accuracy. What needs to be mentioned is that although the method of heavy and positive and positive groups still needs to be developed and improved, in some case studies in the two -dimensional quantum and three -dimensional classic statistical models, this method has revealed other methods that do not have applications that do not have any applications. potential. For example, a two -dimensional Hubbard model related to high -temperature superconductivity, the method of weight and reconciliation group is very beneficial to calculate its optimal change. A series of methods have been used to study this field for disorder and multi -body localization, including the expression of the full spectrum of the energy -based recruitment, or the encoding method of all the national system of one -dimensional multi -body local systems.

3.5 Dynamic average field method

Nowadays, finding a model or method suitable for a strong associated system is still a challenge in the field of condensation of state physics. Because the existing numerical methods have certain limitations, the average dynamic field method has become the object of attention of researchers. Dynamic average field method (DMFT) is a numerical method for the high -dimensional strong association system. This method is based on the complete multi -body problem of solid physical physics to the quantum impurities model. This model is essentially embedded in a small amount of quantum freedom in the bath that meets the self -consistent conditions. This method provides a minimum description of the electronic structure of related materials and treats the Hubbard belt and quasi -particle belt equally. In 1989, Metzner and VOLLHARDT used this method to study the non -mediocre correlation between Fermiko in the endless dimension Hubbard model. When it proposed that when space dimension D → ∞, the Hubbard model can have a high -dimensional limit that can be strictly defined in mathematics. Since then, the study has received widespread attention. In 1992, the Kotliar and Georges research team achieved breakthrough results. They mapped the unlimited Hubbard model to the self -consistent single impurities Anderson model, and then the areas they got from the areas obtained from the areas. It can be amended to return to the original lattice model, and finally determine the thermal library parameters in the single impurities Anderson model through the iterative solution of a self -consuming equation. This mapping is accurate under the limit of unlimited coordinates, and allows people to study related crystal electronic dynamics in the intensity of all interaction. Contrary to the theory of single particles, the average field of DMFT is energy -related, that is, dynamic, which fully considers the rising quantum quantum. As a result, DMFT provides a new theoretical framework for the research -related lattice model. Subsequently, Anisimov and Poteryaev and others combined dynamic average field methods with electronic structure technology to make breakthrough progress. In addition, research by Chitra and KOTLIAR and others shows that the average method of dynamic dynamic field can also be expressed as an approximate value of the precise spectrum density generalization theory (SDFT). After that, this method was rapidly promoted to various types of strong related models and achieved great success.

04

Development and future

At present, the problem of strong -associated quantum multi -body in condensed physics is still a very challenging research field. The strong association between electronics limits the solution from the first principle. Researchers generally establish a model of describing low -energy electrons (such as Hubbard models) to describe systems for specific issues, and then use numerical simulation research system physical properties to reveal physical laws. This section will look forward to the future of related fields in the field of research on the laws of related quantum phenomena and the development of calculation methods. Ⅰ Research areas of potential in the law of quantum phenomenon and mechanisms

(1) High temperature superconducting and gap. At the intercourse of the century, Ginzburg, the Nobel Prize winner, was asked what questions in physics seemed particularly important. In his answer, room temperature superconducting was among the best. For a series of strange metal behaviors appearing in the high -temperature superconducting system, such as linear resistance, charge — spinning separation, etc., the researchers found that it was closely related to the gap. The gap is similar to a band gap, which is actually a area with a very low state density, and its effect on high -temperature superconductors has always received widespread attention. With the advancement of calculation methods and simulation technology, now, the theoretical model of describing high -temperature superconducting and studying the corresponding spectrum functions, including the gap, has become an important issue in condensing state physics.

(2) Electronic -Shengzi interaction. The electronics -electron interaction and electron -vocal interaction of the electronics -electron interaction in the strong corporation cannot be ignored. Significant influence. Holstein模型是一个广泛研究电子—电子相互作用和电子—声子相互作用的模型，现如今已经有很多方法应用于这个模型的研究：如约束路径辅助场量子蒙特卡罗方法、精确对角化、 Monte Monte Carlo Methods and so on. Studying this model and its extension is also an important issue.

(3) Dase of the quantum spin liquid. The quantum spin liquid is regarded as the "quantum disorder" base state of the spin system. In these base states, zero -point rising is very strong, so that the traditional magnetic long program does not exist. Due to a large amount of entanglement, there are quite unique physics in quantum spin liquids, such as non -local area stimulation and topology. At present, few materials have been proven to be quantum spin liquid, so it is necessary to calculate the self -rotation model to avoid the blind test in the experiment.

(4) Non -balanced, non -Ermy quantum system. The system in reality is complex and often deviates from thermodynamic balance, thereby increasing the difficulty of research. The existing theoretical methods are not enough to deal with such problems and need to develop new theories and methods. For the strong associated point model, previous research often pays attention to the closed, with real energy, and Emi is regarded as the core of the research. However, the real physical system is open, and they exchanged energy, particles and information with the external environment, which means that many physical quantities are no longer conservation. Therefore, compared to the Ermy system as a whole, researchers often are more interested in the limited space of the Fei Mimi system. In this case, energy can be exchanged between a specific quantum subsystem and its environment. Including the spelling time symmetry system with gain and loss, the scattered Boli -Einstein condensed body, excitement -polarized tone system, and biological network. Nowadays, the non -Ermy described by the condensation state system provides an effective framework for clarifying non -elastic collision, disorder effects and system -ambient coupling. After the topology insulation is found, the topological research related to condensed state physics has also changed. It is getting more and more important.

Improvement and development of the Ⅱ calculation method

(5) Overcoming the index wall of the quantum multi -system system. In the study of quantum multi -body system, as the number of particles/system scale increases, the System's Hillbert spatial dimension will be divergent, and the complexity will also increase. The performance of today's computers is not enough to completely solve. This brings great difficulties to describe the quantum polygonal wave function or calculation of related physical quantities. Kohn is called the "Index Wall" by the Nobel Prize in Chemistry. For decades, researchers have made a lot of efforts to solve this problem, such as the method of density matrix heavy righteousness group method applied to low -dimensional strong associated systems and quantum Monte Carlo methods. However, there is no way to solve all problems.

(6) Improve negative symbols in the quantum Monte Carlo method. Over the past few decades, the quantum Monte Carlo method has played a role in chemical, condensing state physics, nuclear physics and other fields as an effective tool for solving various discipline problems. However, when the probability of specific quantum configuration in the importance sampling becomes negative, symbolic problems will occur, which greatly limits the application of this method. On the one hand, reducing or even solving the symbolic problem is one of the core topics of calculating condensed physics; on the other hand, Mondaini and others discussed the relationship between symbolic problems in the method of quantum Monte Carlo and quantum critical behavior, so that the relevant related Studies are more challenging.

(7) The development and improvement of the method of heavy and righteousness. Nowadays, the Monte Carlo method has proven to be a non -micro -disturbance method. However, the existence of symbolic issues has limited the use of this method. In 2007, Levin and NAVE proposed the method of weight -to -righteousness. By using the strange value to decompose the contraction of the tensor network, it can be exempted from the symbolic issue and applied to a model with complex weights. The application potential that has not had other methods has the potential for the potential research. And a series of issues, the problem of accuracy when the number dimension increases, the stability problem of the union -caused by non -linearity, and the problem of accurate calculation of the value of the non -Ermy transfer matrix. New research ideas are proposed in the field. (8) Develop and promote dynamic average field methods. After 30 years of development, the average dynamic field is developed, and new innovation is needed to bring breakthroughs. On the one hand, there are continuous research and attempts to promote the theory of dynamic average field to non -balanced systems. The development of this method is limited. On the other hand, the study of strong -associated electronic structures of non -empirical parameters usually uses a linear discrimination and reduction algorithm and dynamic average field method. Because this method needs to set some experience parameters in advance, it cannot fully meet the needs of research. Essence

(9) Computing physics requires further development of algorithms and development software. This is a long -term and huge project that requires sufficient manpower and material investment. With the development of high -performance computers, software that develops and has independent intellectual property rights has become increasingly important for science and technology and material simulation, and this is the case for the country, academic and individuals. In the field of calculating cricket physics, the calculation software has a high degree of commercialization, and has played an important role in material design. Among them, the development of electronic structure computing procedures and its application in material design is an important research direction. Calculation software based on density general letter theory (DFT), such as Vasp, Wien2k, Castep, QE and other software packages Development has reduced the difficulty of using the first principle and methods, and also promoted the development of related fields. At present, Europe is the most active area of ​​the first principle of the first principle, and the United States and Japan also have strong research strength. my country starts late, has less investment in development, and has insufficient development and commercialization of software. So far, it is still difficult to get rid of dependence on foreign software products. To change this status quo, we must strengthen the cultivation of physical methods and software talents, and attach importance to and strongly support the business development research of software.

(10) Machine learning method is applied to quantum multi -body system. With the development of artificial intelligence and big data processing, machine learning methods have been widely used in various areas of physics and various cross -disciplines, which has an important impact on calculating condensed physics. With the intervention of machine learning methods, the new methodology in the field of physics is gradually forming. For example, deep neural network judgments can be used to judge and portray phase change, characterize quantum polyphonic wave functions; use automatic micro -division technology in the tension heavy correction group; improve Monte Carlo update efficiency through machine learning. We expect machine learning methods to provide new research perspectives and ideas for strong affiliated electronics fields.

05

in conclusion

Calculating physics is a discipline that uses computers as a tool, computing methods and software as a means to study material structure and laws. As one of the fastest development areas in the past 20 years, calculating physics from quantum mechanics can design and determine the material system with different functions, structures and components at the atomic level, and provide strong research methods for explaining many physical phenomena. At the beginning of the occurrence, computing physics was mainly used to study material state equations and non -linear dynamics issues. With the enhancement of computer capabilities, the research scope of calculation of physics has become more and more widely, which not only solves the problem that many analytical theories cannot be solved, organically combine theoretical and experimental results, but also predict new physical phenomena, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, physical effects, and physical physics Laws and new materials. With the continuous deepening of research in the field of condensation, the structure and materiality of the materials are becoming more and more abundant, and the research focuses on non -linear issues, random environment and non -analytical solutions. Calculating physics can solve traditional analysis based on the existing theoretical framework or model and solve traditional analysis. The problems that the research cannot be solved has received extensive attention and expectations, and also faces difficulties and challenges. Under the premise of facing electronic strong correlation and quantum rising, the development of new theories and computing methods is urgent and necessary.

At present, in the face of a strong related electronics system, accurate diagonal, numerical reignification groups, quantum Monte Carlo simulation and dynamic average field methods are 4 more commonly used methods. Each method has its own advantages and disadvantages, and has corresponding advantages and limitations while facing different applications. These methods do not meet the needs of researchers' needs for calculating accuracy and computing modeling, such as the existence of index wall problems, quantum Monte Carlo's negative symbol issues, etc. The existing calculation methods still have greatly improved and developed greatly. space. In addition, the laws and mechanisms of related quantum phenomena such as high -temperature superconducting mechanisms, quantum spin liquid, and non -Ermi quantum subsystems are still the topics of the majority of researchers. The research and solution of these topics are closely related to the development of calculating physics. Essence

references

[1] Metropolis n, Rosenbluth a W, Rosenbluth M n. Journal of Chemical PHYSICS, 1953, 21: 1087 [2] Fermi E, Pasta P, Ulam S. 1955, DOI: 10.2172/43766203

[3] Wilson K G. Scientific American, 1979, 241: 158

[4] Wilson K g. Rev. Mod. Phys., 1975, 47: 773

[5] Kang K J, Cheng J P, Chen Y H. Journal of PHYSICS: Conference Series, 2010, 203: 012028

[6] Bernaschi M, Bisson M, Fatica M.

[7] Katsikas G, Sarafidis C, Kioseoglou J. Physica Status Solidi (B), 2021, 258: 2000600

[8] National Natural Science Foundation of China, Chinese Academy of Sciences. Chinese Discipline Development Strategy: Computing Physics. Beijing: Science Press, 2022

[9] SENTHIL T, Vishwanath a, Balents L. Science, 2004, 303: 1490

[10] Lin H, Gubernatis J, G. Computers in PHYSICS, 1993, 7: 400

[11] Hohenberg P, KOHN W. PHYS. Rev., 1964, 136: B864

[12] KOHN W, Sham L J. Phys. Rev., 1965, 140: A1133

[13] KALOS M H, Levesque D, Verlet L. Phys. Rev. A, 1974, 9: 2178

[14] Suzuki M, Miyashita S, Kuroda A. Progress of theoretical Physics, 1977, 58: 1377

[15] Trotter H F. Proceedings of the American Mathematical Society, 1959, 10: 545

[16] Handscomb D C. Mathematical Proceedings of the Cambridge

Philosophical Society, 1962, 58: 594

[17] Evertz H G, LANA G, Marcu M. Phys. Rev. Lett., 1993, 70: 875

[18] BlankenBecler R, Scalapino d j, Sugar R l. Phys. Rev. D, 1981, 24: 2278

[19] Berg E, Metlitski M A, Sachdev S. Science, 2012, 338: 1606

[20] White S R. PHYS. Rev. Lett., 1992, 69: 2863

[21] Schollwöck u. Rev. Mod. Phys., 2005, 77: 259

[22] Levin M, NAVE C P P. Phys. Rev. Lett., 2007, 99: 120601

[23] ORús R. Nature Reviews Physics, 2019, 1: 538

[24] Metzner W, VOLLHARDT D. PHYS. Rev. Lett., 1989, 62: 1066

[25] Georges A, Kotliar G. PHYS. Rev. B, 1992, 45: 6479

[26] KOTLIAR G, Savrasov S Y, haule k. Rev. Mod. PHYS., 2006, 78: 865

[27] Georges A, Kotliar G, krauth w. Rev. Mod. PHYS., 1996, 68: 13

[28] zhang y x, chiu w t, Costa n c. Phys. Rev. Lett., 2019, 122: 077602

[29] han Z, Kivelson s a, yao h. Phys. Rev. Lett., 2020, 125: 167001

[30] Clark L, Abdeldaim A H. Annual Review of Materials Research, 2021, 51: 495

[31] Hosseini M V, Askari M. Scientific Reports, 2021, 11: 22206

[32] El-Ganainy R, Makris K G, Khajavikhan M et al. Nature physics, 2018, 14:11

[33] XU Z, chen S. PHYS. Rev. B, 2020, 102: 035153

[34] Gong Z, Ashida y, kawabata k. Phys. Rev. X, 2018, 8: 031079

[35] zhang X Z, SONG Z. PHYS. Rev. B, 2020, 102: 174303

[36] Mondaini R, Taraat S, Scalettar R T. Science, 2022, 375: 418

[37] AOKI H, Tsuji N, Eckstein M et al. Rev. Mod. PHYS., 2014,86: 779

Reprinted content only represents the author's point of view

Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences

If you need to reprint, please contact the original public account

Source: China Physical Society Journal Network

Edit: Tibetan idiot

- END -