Do you really understand the problem of coin flip?

01

Origin of a story

There are N coins, and each coin may be facing the front or back.

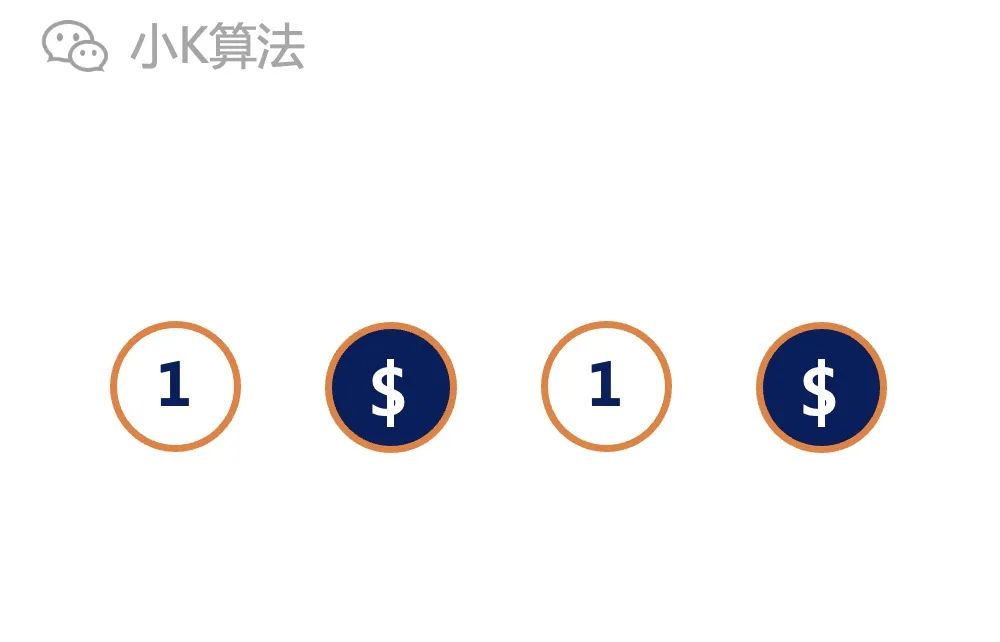
If a coin is flipped each time, after a certain number of flipped, all the coins can be facing up or upward, that is, the state can be consistent.

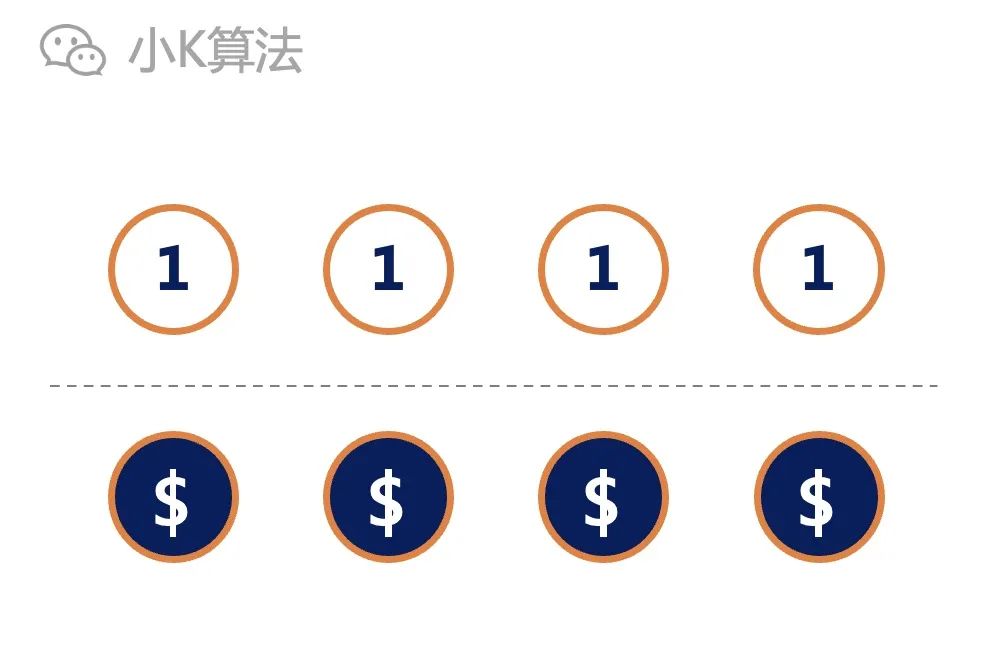
Is there a fixed number of K, so that no matter what kind of state in the beginning, it can just turn on the K times to achieve the state of all positive or opposite faces? If you exist, what is the smallest K?

02

analyze

Let's start with simple scenes.

If there is only one coin, it can be positive or opposite, because there are no other comparison, so the state is consistent. No need to flip, then the smallest K is 0.

If there are 2 coins, there may be the following three states at the beginning: 2 positives, 2 reverse sides, 1 positive and 1 reverse.

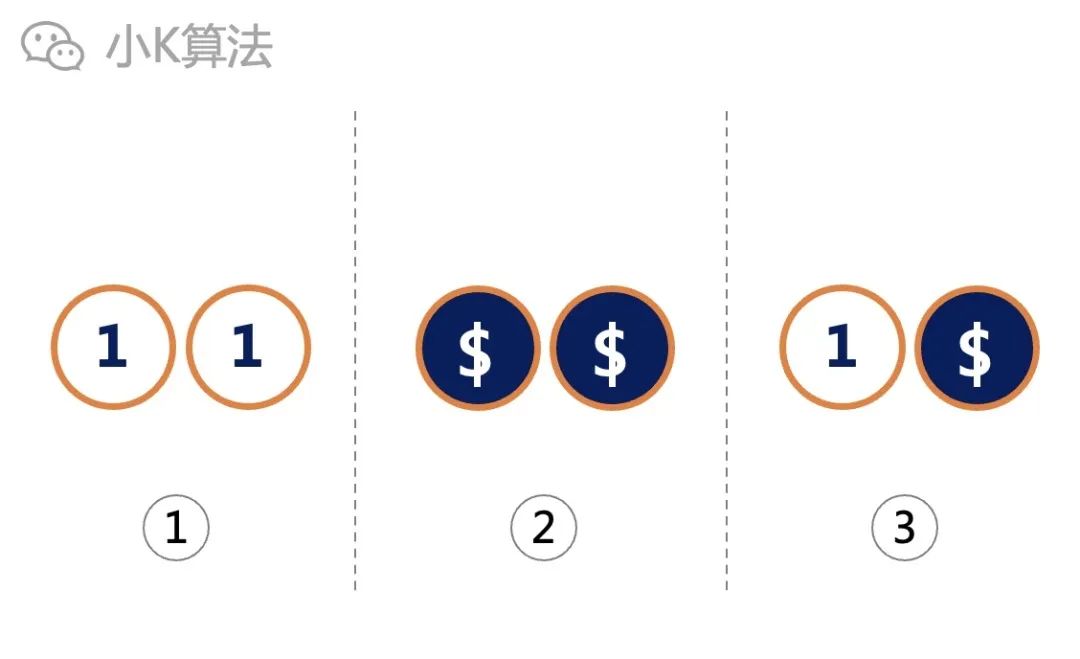
For the above 1 and 2 states, there is no need to flip, and the third one needs to be flipped at least once. If all are flipped once, the two states in the previous two will be inconsistent, so you cannot find a fixed number of flip times K.

If there are 3 coins, there is no need to consider the initial state, the minimum is 0 times.

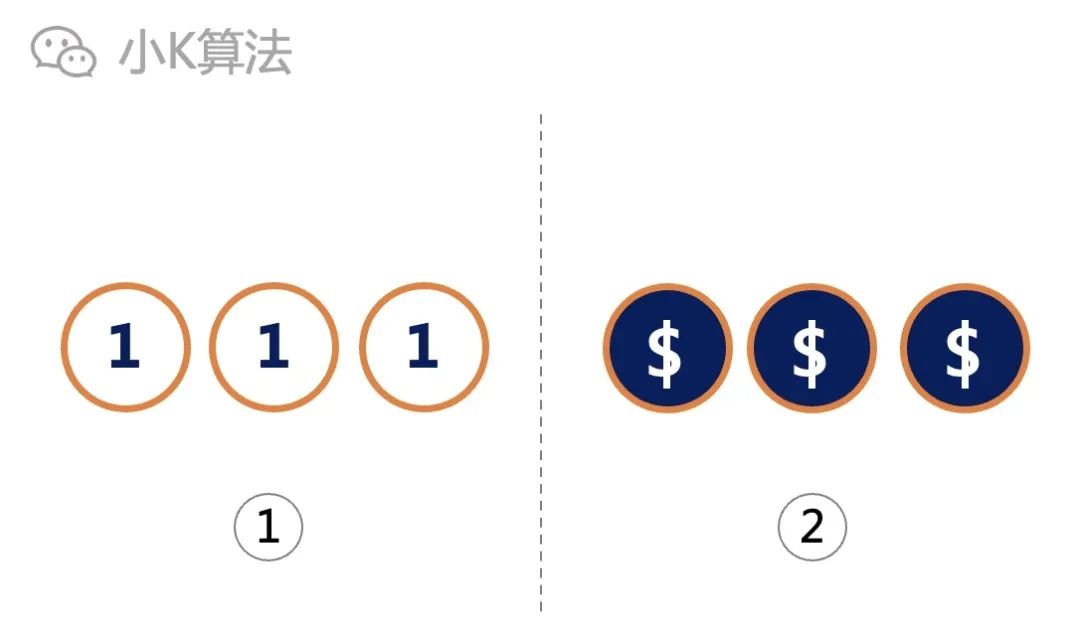
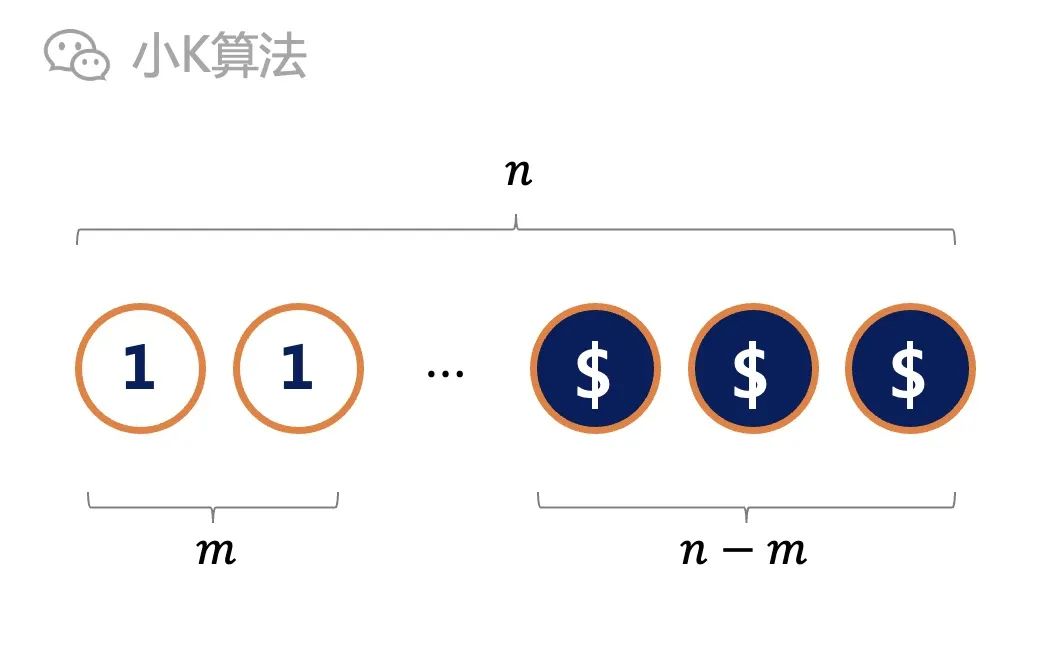
The main considerations are inconsistent, such as 1, 2 ... M inconsistency.

It can be seen that if n coins are positive, there must be N-M reverse, and it can Small, because it is simpler.

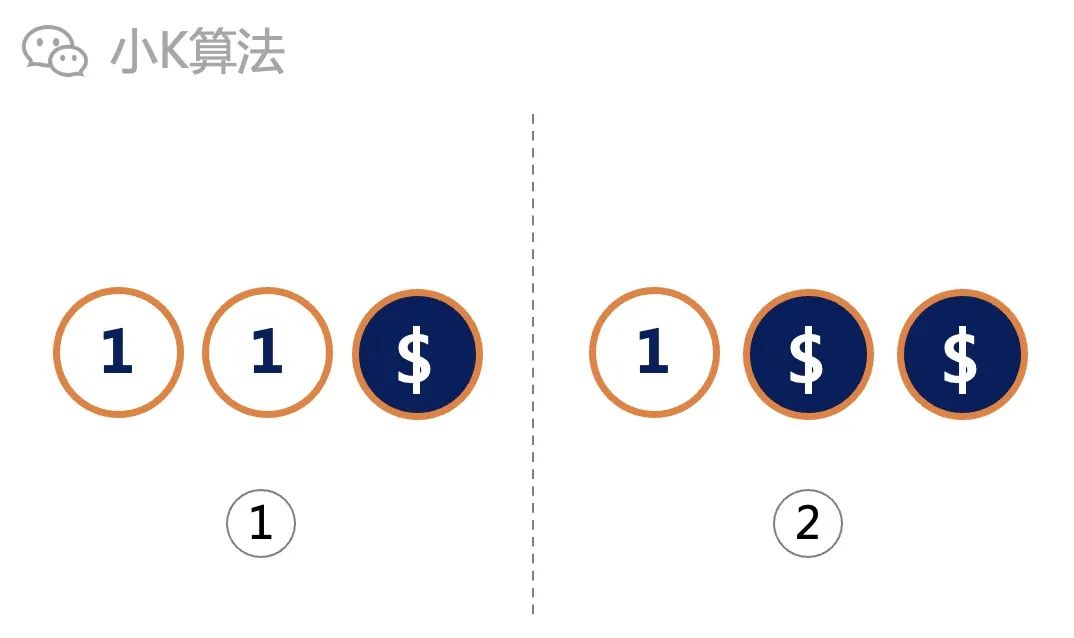
Back to the situation of the three coins above, you only need to consider one positive and two positives.

If you flip it once, you can make all the same, but the same situation must be turned once in the initial situation, which will definitely cause inconsistencies, so it will not work once.

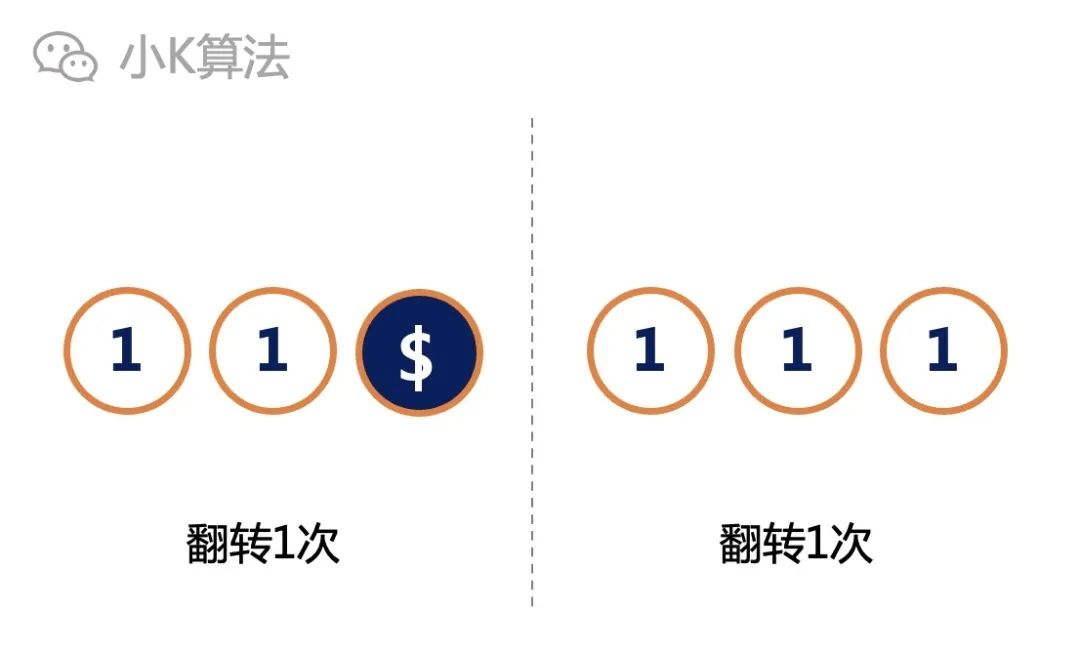
If both flip twice, you can definitely. If one front, turn the other two reverse; if two positives, just flip the two positives directly; if all the same is the same, it will still not change the state of consistent twice if it is all the same. So the minimum k of 3 coins is 2.

Do you see the regularity here, don't look down first, think about 2 minutes, 3,2,1 ...

03

law

When you start to summarize the law and extract feature information, don't limit your imagination and diverge your thinking.

1. First of all, for any coin, the state of turns will be changed several times, and the state must not change the state several times.

Since the flipping occurred several times, why is it still to flip, of course, for the number of numbers, because the requirements must be just flipped.

2.K must be even. If the initial state is consistent, a certain state will change a certain state several times to become inconsistent, so K cannot be a strange number.

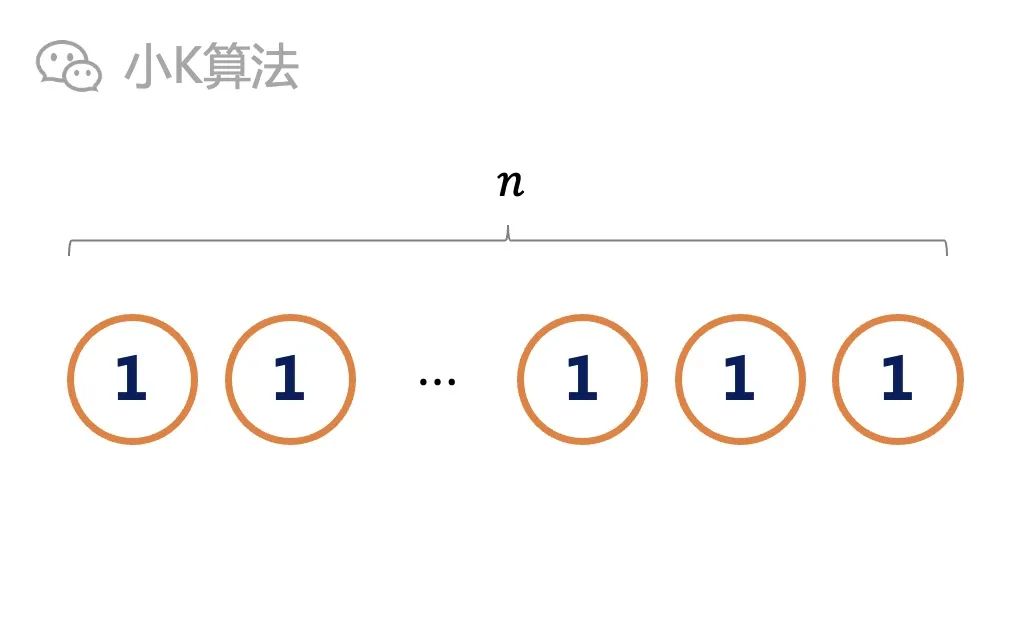
3. If it is even, you will not find such K.

For example, there is only one reverse side in the following scene, with n-1 positive. 1 and n-1 are strange numbers, so whether it is flipped to the front or the opposite side, it needs to be flipped for several times. It is impossible to consistent for several times, so N is not solved when even.

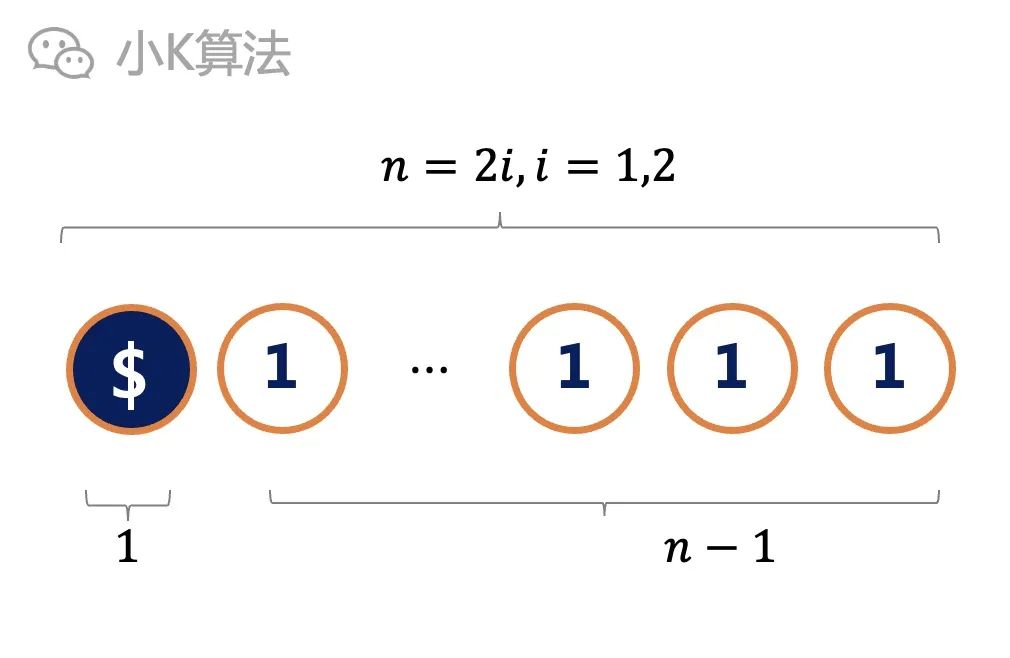
4. The most important thing is that there must be a solution for n as a strange number. What should the smallest K be?

n is a odd number, so the front and negative are definitely a strange one.

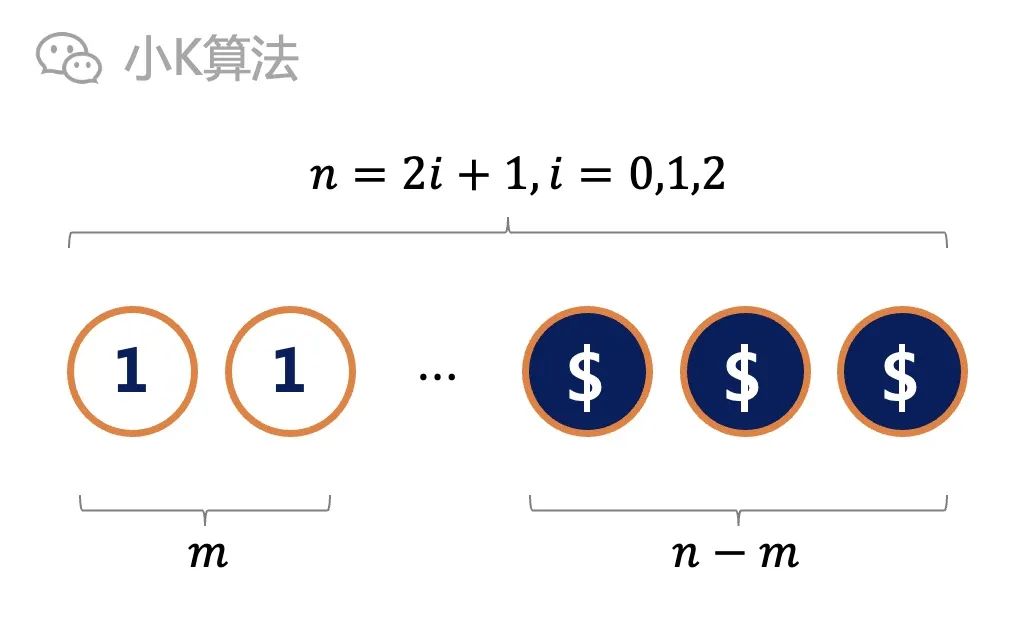
Considering this extreme situation, there is only one reverse side, n-1 positive, and N-1 is even.

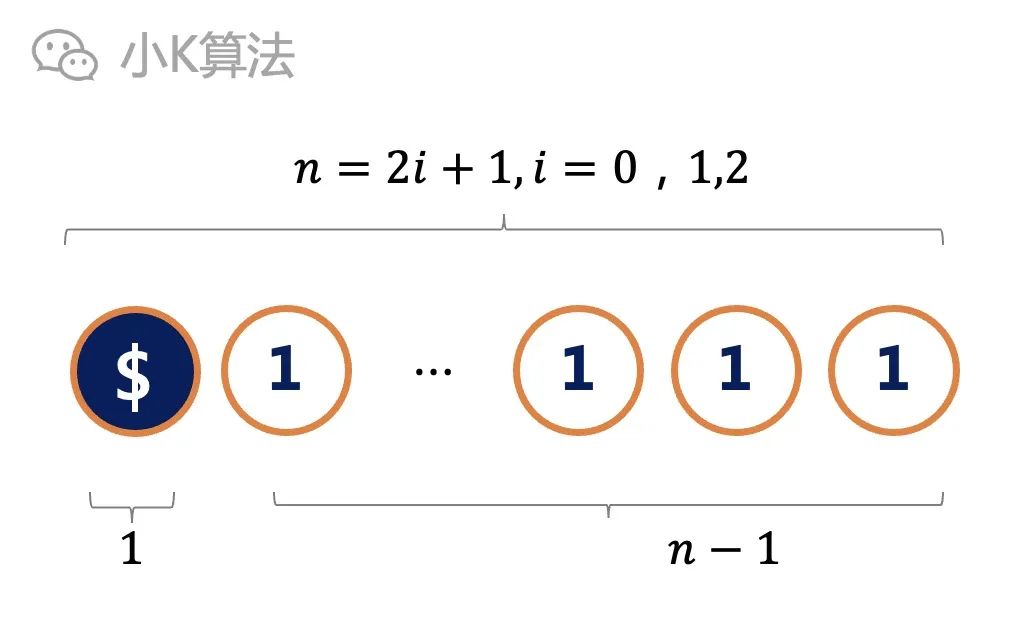
If all of them are positive in the end, you can only flip the opposite side, but the flipping occurs without changing, obviously not. So only in the end, you must turn the remaining n-1 front, at least N-1 times.

Well, the rules are found, let's start with.

04

Code

Of course, the difficulty of this problem is not in CODING, which is just a subsidiary after the successful reasoning.

if ((n1) == 0) Printf ("Nosolut!!

"); Elseprintf ("%D

", n-1);

05

Summarize

This problem is mainly to find the rules in essence and reasoning a lot. The results are extremely simple, but these reasoning cannot be turned around. In fact, there are many seemingly complicated problems, and the final conclusion is very simple. There is an experience to share with everyone. If you find that you are very complicated when you solve a problem, you need to consider many branches. At this time, I can probably guess that 90%of your method is wrong, because the righteousness is always very very solved very much very very very very very very very very solved very. Elegant and simple. (If it is not elegant, it must not be a positive solution)

Reprinted content only represents the author's point of view

Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences

- END -