The masterpiece of physics is buried in the unattended meteorological literature

Many years later, physicists will talk about the dissertation of Lorenz's discussion of these equations- "the beautiful masterpiece". For the first time in history, Lorenz's images were clearly showed to us, saying "this is complicated" what it means. All the rich meaning of chaos is there.

Written article | James Gleick

Translation | Lou Weishan

In the 1950s and 1960s, there was an unrealistic optimism of weather forecast everywhere. The newspapers and magazines are full of hopes for meteorological science, not only the weather forecast, but also artificially affect weather and weather control. There are two technologies that are becoming increasingly mature, which are electronic computers and artificial satellites. An international cooperation project called the Global Atmospheric Research Program is also preparing to make full use of them. One of the thoughts at that time was that human society will be liberated from the impermanence of the weather, and from its victims to its master. The short -range dome will cover the corn field. The aircraft will spread directly into the cloud. Scientists will learn how to make rain and stop rain.

The father of this trend of thought is von Neumanman. One of the functions he wanted when he designed his first computer was to control the weather. He convened a group of meteorologists and promoted his plan to the general scientific community. For his optimism, he has a specific reason for mathematics. He noticed that a complex power system can have some unstable points -some critical points, where to push it lightly, it will cause major consequences, just like the ball on the top of the mountain. And von Neumann's imagination that with the help of computer, scientists can calculate the act of the formula of fluid movement in the next few days. Then a central committee composed of meteorologists will send planes to disperse cigarettes or broadcast clouds, thereby pushing the weather to the desired direction. But von Neuman ignored the possibility of chaos, and every time it would be unstable.

By the 1980s, a huge institution was specially spent to pursue the goal of von Neumanman, at least the weather forecast part of it. In a square box building in the suburbs of Maryland (close to Washington), the top of the United States in the square box building with a simple appearance, the roof is full of radar and radio antenna. The weather model of their supercomputers is similar to Lorenz's most basic spiritual. Compared with the Royal -McBP -30, it can perform sixty multiplication computing per second. The power of a CDC Cyber ​​205 large machine is a floating -point calculation of one million times per second. Compared with Lorenz's satisfaction in the twelve equations, modern global weather models handle systems with 500,000 equations. Their model understanding is how the air is released and absorbed with heat. Digital wind will be affected by digital mountains. Each hour, data from various countries around the world will be brought together here. The National Meteorological Center produced the world's second best weather forecast.

The best weather forecast comes from the town of Reading in England, a university town one hour from London. The European Medium Weather Forecast Center is located in a building covered by trees. This is a modern brick and glass building with an United Nations style with gifts from various places. It was the product of the prosperity of the European common market. At that time, most Western European countries decided to gather their respective talents and resources in order to make more accurate weather forecasts. The Europeans attribute their success to their young talents (no civil servants) and their Krey supercomputers (it always seems to be an advanced model of the computer used by Americans).

The weather forecast marks the beginning of the use of computers as a complex system modeling, but this is undoubtedly not its end. The same technology has also helped scientists and social scientists in many areas to make predictions. From the small -scale fluid flow that the pusher designer cares about to the large -scale financial flow that economists care about. In fact, by the 1970s and 1980s, the use of computers for economic predictions has become very similar to global weather forecasts. Various models will be penetrated in a complex but non -arbitrary network composed of the equation group. Through they will transform the measurement of initial conditions (whether it is atmospheric pressure, or currency supply) into a simulation of future trends. Researchers hope that the results will not deviate from reality because of many inevitable simplified assumptions. If a model does get an obvious outrageous result (such as the flood of Sahara, or the interest rate of three times), the researchers will adjust the equation group so that the result will be on track. In practice, the economic model has been repeatedly proven to be difficult to make a reliable prediction in the future, but there are still many people. They should have been more clear about this, but they are as if they are convinced of these results. The prediction of economic growth rate or unemployment rate often implies that people have accurately reached two or three decimals themselves. Government and financial institutions often pay for such predictions and take action on the basis of them, which may be due to necessary or lack of other better choices. Perhaps they know that variables like "consumer confidence" do not have a good measurement like "humidity", and for the changes in political and fashion, we have not found the differential division equations that can perfectly portray them. But few people realize how fragile the process of various streaming models on the computer is itself. Even if the data is quite reliable, and the laws that dominate them are pure physics, just like the weather forecast. Computer modeling has indeed succeeded in changing the weather forecast from an art to a science. The assessment of the European Medium Weather Forecasting Center shows that by the statistical view of the predictions that are better than nothing, the world can reduce the loss of billions of dollars each year. But more than two or three days, even the best weather forecast in the world is just guessing; and more than six or seven days, they become worthless.

The butterfly effect is the median. For small -scale weather phenomena (from the perspective of a global weather forecast, "small -scale" may mean thunderstorms and snow storms), any prediction will deteriorate quickly and useless. Errors and uncertainty are constantly accumulated, and they are continuously enlarged in a series of turbulent phenomena of different sizes (from dust rolls and 飑 to huge vortexes that can only be seen through artificial satellites).

The modern global weather model uses data sampled from a grid of a 100 -kilometer grid between a grid point, and even so, some initial data still need to be obtained by guessing, because ground stations and artificial satellites cannot be everywhere. All observed. However, you may wish to imagine that the entire earth can be covered with sensors. They have a horizontal interval of thirty centimeters and a vertical interval of 30 centimeters. Then imagine that each sensor can give a complete and accurate reading about temperature, air pressure, humidity, and other physical quantities that meteologists want to know. Then at noon, an infinitely powerful computer read all these data, and calculated the weather conditions of the next minute (12:01, 12:02, 12: 03, ...).

At that time, the computer will still be predicted that one month later, the town of Princeton, New Jersey is sunny or rain. At noon, there will be a random rise in the space between the sensor, which is not known to the computer, that is, the slight deviation of the average value. By 12:01, these ups and downs will create tiny errors in thirty centimeters. These errors will soon accumulate at the scale of three meters, so that it will cause significant differences until the scale of the entire earth will cause significant differences.

Even for senior meteorologists, all these are illegal. An old friend of Lorenz was MIT's meteorologist Robert White, who later became the first director of the National Oceanic and atmospheric Administration. Lorenz explained to him the butterfly effect, and what he felt that it could mean long -term prediction. White gave an answer from von Neumanman. "Prediction, irrelevant," he said, "this is weather control." His idea is that small artificial effects in the scope of manpower and scope will cause the weather changes on the large scale we want.

Lorenz thinks not. Indeed, you can change the weather. You can make it different from the original appearance. But if you do this, you can never know what it would look like. This is like washing a pair of already washed playing cards again. You know this will make you change your luck, but you don't know if your luck will become better or bad.

Lorenz's discovery is an accident, one of the countless accidents since Archimede and his bathtub. Lorenz has always been the type of "Yurica". This accident discovered that it was just a place he had never left. He is going to find out what it means to understand the way of various fluid flows scientifically, and explore the meaning of the discovery in depth.

If he stopped at the butterfly effect at the beginning, a description of predictability to concession to completely randomly random, then Lorenz may have revealed only a very bad news. But Lorenz saw in his weather model more than just randomness. He saw a fine geometric structure, a kind of random order. After all, he is a mathematician installed as a meteorologist, and at this time, he started to live a double -sided life. He will write pure meteorological papers. But he will also write pure mathematics papers, but only a little bit misleading the weather topic of people as the opening whites. In the end, such opening remarks will disappear completely. He turned more and more to such systems of mathematics. These systems could not find a state -of -state state, and almost repeated himself, but he had never done it completely. Everyone knows that the weather is such a system -non -cyclical. Other similar examples are all in nature: the number of animal population that almost rules is ups and downs, with the epidemic disease that is close to the periodic schedule and the fading, so, and so on. If the weather does come to an exact state of a certain state that has been experienced before, and each wind is exactly the same as each cloud, then it may be repeated by itself. At this time It becomes ordinary.

Lorenz realized that there was a connection between the weather unwilling to repeat himself and the weather forecaster that it must predict it -a connection between non -periodic and unpredictable. It is not easy to find a simple and simple group group that he will find. At the beginning, his computer model tended to fall into a repeat cycle. But Lorenz tried a variety of slightly complicated, and eventually added a temperature difference in the direction of something (corresponding to the differences in the real world, such as the differences in the heating and temperature of the North American coast and the Atlantic Ocean). After the equation was successful. Repeat disappear.

The butterfly effect is not an accident, but a necessary. Lorenz reasoning, envisaging small disturbances is not to accumulate expansion in the system, but to maintain such a small state. Then when the weather becomes any state that it has experienced before, it will maintain this. Close to this state. In fact, such a cycle will be predictable -therefore is also boring. In order to generate colorful and universal weather on the earth, you can't imagine something better than a butterfly effect.

The butterfly effect is also crowned by another technical name: sensitive dependence on the initial conditions. The sensitive dependence on initial conditions is not a new concept. It is reflected in folk stories:

Laren one nail, lost a iron hoof;

One less iron hoof, lost one battle horse;

Laren horse horse, lost a rider;

With one less knight, lost a victory;

With one victory and lost a kingdom.

Like in life, in science, as we all know, there can be a variable point in a series of incidents that enlarge the small changes. But chaos means that such points are everywhere. They are everywhere. In a system like weather, sensitive dependence on the initial conditions is an inevitable result of a way to interact with large scale and large scale.

His colleagues were surprised to grasp the non -periodic and sensitive dependence on the initial conditions at the same time, and what he used was only a toy model of the weather: twelve equations, and then calculated it over and over with the mechanical efficiency. So how can such richness and unpredictability (such chaos) emerge from a simple decision -based system?

Lorenz temporarily put down the weather and tried to find a more simple way than it to generate this complex behavior. In the end, he found this way in a system that is only composed of three equations. These equations are non -linear, that is, the relationship they represent is not strictly proportional. Linear relationship can be expressed as a straight line on the figure. It is also easy to understand: more good. The linear equation group is solution, which makes them suitable for textbooks. The linear system also has an important component advantage: you can disassemble them, and then assemble them together -all parts are available.

Non -linear systems are generally irreplaceable and indispensable. In the fluid system and mechanics system, non -linear items are often some characteristics that people want to ignore when trying to get a simple understanding. For example, friction. In the absence of friction, the energy required for an ice hockey can be represented by a simple linear equation. In the absence of friction, the relationship becomes more complicated, because the required energy depends on the speed of the ice hockey. Non -linear means that the behavior of participating in the game itself will change the rules of the game. You cannot give friction a constant importance because its importance depends on speed. The speed depends on the friction. This kind of dependence makes it difficult to calculate non -linear, but it also creates a variety of behaviors that are not seen in linear systems. In fluid dynamics, everything can be attributed to a classic equation -Navavi -Stokes equation. This is a simple miracle that connects the speed, pressure, density and viscosity of fluids, but it happens to be non -linear. Therefore, the nature of these relationships often becomes clearly determined. Analysis of a non -linear equation like Navavi -Stocks equation seems to be walking in a maze, and its walls will re -arranged with every step of you. As von Neuman himself said: "The characteristics of the equation ... change at the same time at all levels: the number and degree of the number of times. Therefore, the tricky mathematics problem must be followed." The Wi Stocks equation does not contain non -linear devil, then the world will become large, and science will not need chaos. The three equations of Lorenz are inspired by a specific type of fluid movement: the rise of thermal gas or liquid, that is, the current. In the atmosphere, the air close to the ground rises in heat; on the surface of the hot asphalt and radiator, the heat is rising, like ghosts. Lorenz is also happy to talk about the current of a cup of hot coffee. According to his statement, this is just one of us who may want to predict its future insecure fluid power. How can we calculate how fast a cup of coffee will cool? If the coffee is only warm, the calories will be slowly dissipated without any fluid power movement. At this time, coffee is maintained in a state. But if it is hot enough, the current process will bring hot coffee from the bottom of the cup to a lower temperature. Just add some cream to the cup, the stream in coffee will become clearly visible. The white vortex can be very complicated. But the long -term fate of such a system is obvious. As the heat is constantly dissipated and the friction has slowed the speed of the fluid, the entire exercise must eventually inevitably stop. Lorenz joked at a group of scientists: "It may be difficult for us to predict the temperature of coffee after one minute, but we should not be difficult to predict its temperature after an hour." The motion equation group must be able to reflect the fate of the system. They must be scattered. The temperature of coffee must gradually tend to room temperature, and the speed must be zero.

Lorenz chose a set of described equations, and tried to simplify it, abandon everything that might be wrong, so that it was simple to get rid of reality. There was almost no shadow left by the original model, but he did retain non -linearly. In the eyes of physicists, these equations look very simple. You will glance at it (many scientists later are indeed), and then say, "I can solve it."

"Indeed," Lorenz said calmly. "When you see them, you will tend to think like this. There are some non -linear items in them, but you think there must be some way to bypass them. Just can't do it. "

The simplest textbook -style pair is out of a fluid -filled box. One smooth bottom of the box can be heated, and the other smooth top surface can be cooled. The temperature difference between the bottom of the hot and the top of the cold controls the movement of fluid flow. If the temperature difference is small, then the entire system remains still. At this time, the heat flows from the bottom to the top through the thermal conductivity, as if flowing through a metal, which is not enough to overcome the natural tendency to maintain the macro macro. In addition, the entire system is stable. Any random exercise (such as a graduate student tapping experimental equipment) will slowly disappear, causing the system to return to its state.

E Adolph e. Brotman

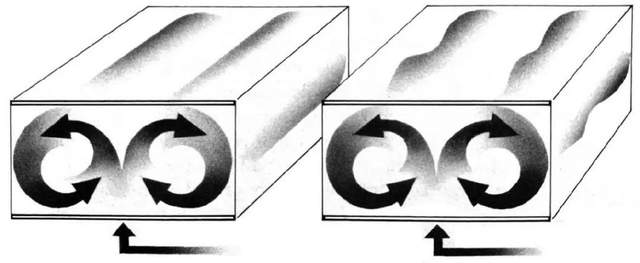
Rolling fluid: When a liquid or gas is heated at the bottom, the fluid tends to form a cylindrical vortex (left) by self -tissue. The heat flow rises on one side, gradually loses heat, and then sinks on the other side -this is the process of the current. After further heating (right picture), a kind of instability begins to appear, and the turbine starts to swing along the long shaft of the cylindrical body. At a higher temperature, fluid flow becomes dull and disordered.

But if you increase the heating intensity, the new type of behavior will appear. As the fluid at the bottom is heated, its volume expands. As its volume expands, its density becomes smaller. As its density becomes smaller, it is relatively light, enough to overcome friction, thereby rising to the top. In a carefully designed box, cylindrical vortex will appear, one of which is the heating of the heat flow, and the other side is the cold flow sinking supplement. From the side, the entire movement constitutes a continuous circle. Outside the laboratory, nature often creates its own drav cells. For example, when the sun is heating on the surface of the desert, the rolling airflow will create a mysterious model in the accumulated clouds above or the sand pile below. Further increase heating intensity, the behavior of fluids becomes more complicated. The rolls will start to twist and swing. Lorenz's equations are too simplified, which is not enough to model such complexity. What they abstract is only a characteristic of the real world convection: the heat flow rises and the cold stream sinks, rolling like a ferris wheel. These equations take into account the speed and heat transfer of this movement, and these physical processes are interactive. As the heat flow rises along the circle, it will contact other relatively cold parts to start losing heat. If the speed of exercise is fast enough, then the bottom fluid will not lose all additional heat when it reaches the top and starts to sink along the other side of the turbine, so it will actually start to hinder the motion of other thermoscopy behind it.

Although Lorenz's system has not been fully modeling for the current, it turns out that it can still find some exact correspondence in the reality system. For example, his equations accurately describe an old -fashioned generator. As the ancestor of modern generators, a disc generator generates current through a disc in a magnetic field. Under certain conditions, a dual -disc generator can reverse the current in the line. After Lorenz's equations have become known to more people, some scientists have proposed that such a generator behavior may explain another weird reversal phenomenon: geomagnetic field. People already know that in the history of the earth, this "geomagnetic generator" has reversed many times, and the interval between these reversal looks raxy and difficult to explain. In the face of such irregularities, theoretical researchers usually try to find explanations outside the system and put forward reasons such as meteorites impact. But perhaps the geomagnetic motor has its own chaos.

Another system that can be accurately described by Lorenz's equations is a certain kind of waterwheel, which is a mechanical ratio of the flowing circular motion. At the top, the water flowing into the water bucket hanging on the edge of the waterwheel. Each water bucket leaks the water through a small hole below. If the water flow is slow, then the highest water bucket will never accumulate enough water, not enough to overcome the friction; but if the water flows faster, the weight of the water bucket at the highest point will drive the water truck to start to rotate. Rotation may continue in the same direction. Or if the water flows so fast, the heavy water bucket crosses the lowest point to the other side, so the entire waterwheel may slow down and stop, and then rotate backwards, in one direction in one direction, in the other direction.

Faced with such a simple mechanical system, the intuition of physicists (the intuition of chaos in the past) will tell him that in the long run, if the water current keeps at a constant speed, a fixed state will evolve. Either the waterwheel rotates at a constant speed, or it oscillates it stably, in a constant interval in one direction, and in the other direction. But Lorenz discovered that this was not the case.

E Adolph e. Brotman

Lorenz's waterwheel: The first famous chaos system discovered by Edward Lorenz corresponds to a mechanical device: a waterwheel. This simple device is proven to generate unexpected and complicated behaviors.

The rotation of the waterwheel has some attributes that are similar to the rolling cylindrical body in the process of streaming. Waterwheels are like a cross -section of cylindrical body. Both systems are driven by uniform speed (water or calories), and both dissipate energy (fluid heat loss, and water bucket leaks). In the two systems, long -term behavior depends on the strength of driving energy.

Water flows in at a constant speed. If the water flows slowly, the highest water bucket will never accumulate enough water, not enough to overcome the friction, and the entire waterwheel will not start to rotate. (Similarly, in the fluid, if there is not enough calories, it is not enough to overcome the stickiness, and the fluid will not start to move.)

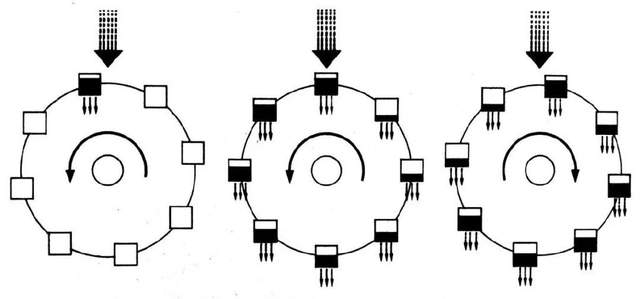
If the water flows faster, the weight of the water bucket at the highest point will drive the waterwheel to start to rotate (left). The entire waterwheel will enter a uniform speed rotation in the same direction (middle map).

But if the water flows faster (right), the rotation will become chaotic due to the non -linear effect of the internal system. As the water bucket passes through the water flow, the amount of water they can undertake depends on the speed of rotation. On the one hand, if the waterwheel turns fast, there is not much time to pick up the water. (Similarly, there is not much time to absorb calories in the fluid in the fast rolling convection.) On the other hand, if the waterwheel turns quickly, the water bucket will come to the other side before the water leaks. Therefore, the heavy water fighting on the other side will cause the rotation to slow down and even reverse.

In fact, Lorenz discovered that in the long run, rotation will reverse multiple times, and never appear a stable frequency, and never repeat itself in any predictable mode.

The three equations (together with their three variables) completely describe the movement of this system. Lorenz's computer outputs these three variables that are constantly changing: 0–10–0, 4–12–0, 9–20–0, 16–36–2, 30–66–7, 54–115 - 24, 93–192–74. With the push of time in the system, five time units, one hundred, one thousand, these numbers are ups and downs. In order to use data to get an intuitive image, Lorenz uses the three numbers of each group as the coordinates to determine one point in the three -dimensional space. As a result, the sequence of the number generates a sequence of a point, a continuous rail line of the system behavior. Such a rail line may come to a place, and then terminate, which means that the system will eventually enter a fixed state. At that time, variables about speed and temperature will no longer change. Or the rail line may constitute a ring, which means that the system finally enters a periodic to repeat its own behavior mode.

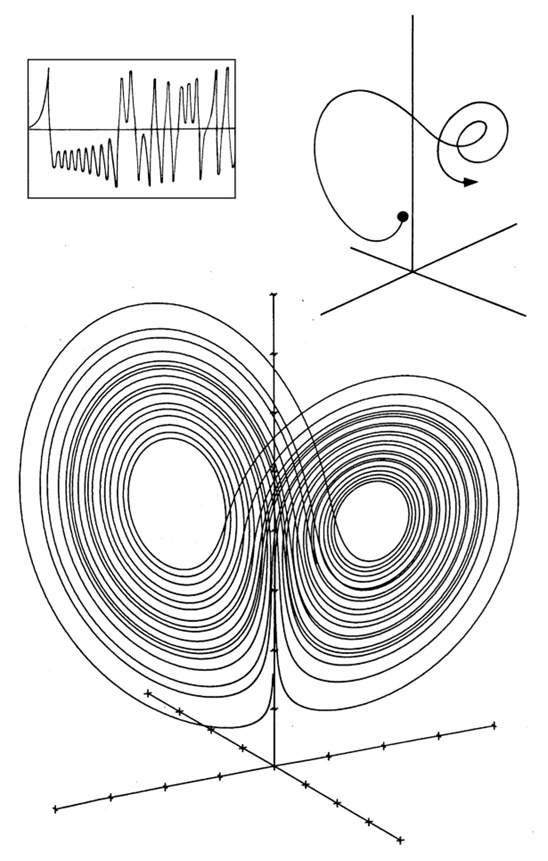
Lorenz's system does not belong to these two situations. Instead, its image shows an infinite complexity. It always stays within a specific boundary, and does not take a step in the thunder pool, but it has never repeated itself. It generates a weird and unique shape -the double snail line in a certain three -dimensional space is like a butterfly stretching the wings. This shape reveals pure disorder, because there is no point or point of which is repeated. But it also reveals a new type of order.

Many years later, physicists will talk about the dissertation of Lorenz's discussion of these equations- "the beautiful masterpiece". At that time, it was said to be an ancient scroll, which contained an eternal machine. In tens of thousands of technical documents discussed in chaos, there are almost no papers more often cited than the article "Decisive Non -Discose Stream". For many years, no object will be compared to the mysterious curve described in the paper, that is, the double snail line that was later known as Lorenz's attraction, which inspired and spawned more illustrations, and even animation. For the first time in history, Lorenz's images were clearly showed to us, saying "this is complicated" what it means. All the rich meaning of chaos is there.

. James P. CrutChfield / Adolph E. Brotman

Lorenz attracted man: This magical image similar to owl masks or butterfly wings has become a symbol of the early explorer of chaos. It reveals the fine structure behind a disorderly data stream. Traditionally, the continuous change of a variable can be expressed as a so -called time sequence (upper left). But in order to show the continuous changes between the three variables, this requires a different technology. At any given time, the value of the three variables determines the position of one point in the three -dimensional space; as the system changes, the movement of this point represents these changing variables.

Since the system will never repeat itself, its trajectory will never intersect. On the contrary, it is always around. The movement of the attractive child is abstract, but it still conveys some characteristics of the real system movement. For example, from the wing of the attraction to the other wing, it corresponds to the reversal of the wartar or the movement direction of the flow.

However, at the time, almost no one could see this. Lorenz once described his discovery to William Marcus (a MIT applied mathematics professor, also a polite scientist, has extraordinary appreciation ability for colleagues). Marcus laughed after listening: "Ed, we know (we know clearly), the flow of the fluid will not happen at all." Marcus told him that the complexity would undoubtedly weaken slowly, and the system eventually eventually eventually. It will tend to stabilize and regular movement.

"Of course, we did not grasp the key at the time," Malcus later (that is, he actually set up a Lorenz water vehicle in his basement laboratory in his basement laboratory to " After many years after preaching), "Ed thought at the time was not our physics at that time. What he thought was a general or abstract model, and the behavior he showed At some levels of the external world, he couldn't tell us that. Only after the matter, we realized that he must be such a point of view. "

At that time, few outsiders realized how much the scientific community had become each other; it was like a warship, and one of the water tight cabins to make each cabin isolate each other and densely water. Biologists do not need to pay attention to mathematical documents, and there are enough things to read -in fact, molecular biologists do not need to pay attention to population biology, and there are enough things to read. Physicists also spend their valuable time than browsing meteorological journals. Some mathematicians were excited to see Lorenz's discovery; and in the next ten years, many physicists, astronomers and biologists have been looking for things like this, and sometimes they have re -re -re -re -re -re -re -re -re -reinforcing themselves. Discovered it. But Lorenz was a meteorologist, and no one thought of going to the 103rd of Volume 20 of the Atmospheric Science Journal to find chaos.

This article is selected from the "Chaos" (Edition 2021 of Renmin Post and Telecommunications Press), which is added by the editor.

- END -