The "colorful black" of the crazy designer was so beautiful in the mathematical world!

Author:Institute of Physics of the Ch Time:2022.08.26

Have you ever heard the "colorful black" stalk? The word originated from a blog post that became popular on Weibo. Tucao customers want "whether the logo can zoom in at the same time", "Can you change a colorful black", which has aroused the resonance of many designers Essence

Let's share the "colorful black" in the mathematical world today.

At first glance, is it a bit "colorful"?

Forming is a "infinite cycle" model that repeats yourself at different scale. This repeated nature is called similar. Forming is considered infinitely complicated, that is, if you can continuously enlarge a fractal picture, you can always see the same structure.

The terminology of division was created by Mandaelo in 1975, which originated from Latin "Fractus".

"Forming Form"

Most of the fascinating artists fascinated by artists are produced by non -linear iterative iterations. Mande Beroo, named by mathematician Mandaelo, is a fractal generated by non -linear iteration methods.

Benoîtb.mandelbrot is a descendant of the Lithuanian Jewish family born in Poland. He moved to Paris with his family at the age of 12, and spent most of his life in the United States.

Mandaelo loved mathematics and obsessed with geometry in his childhood. Later, his research scope was very wide. He studied cotton prices, stock rising, and vocabulary distribution in language. From physics, astronomy, geography to economics, physiology ... all involved.

He has been doing research in IBM, and has been in Harvard Economy, in Yale, and in Einstein School of Medicine. Perhaps these research experience in multiple fields that seem to have no intersection have made him create a fractal geometry of cross -disciplinary disciplines.

Mandaelo is talking to the public

One night in the summer of 1975, Mandaelo was thinking about a statistical phenomenon he encountered in the field of cosmic studies. Since the 1960s, this seemingly chaotic and broken statistical distribution phenomenon confused Mandaelo. It has its shadow in population distribution, biological evolution, natural phenomenon and landforms, and financial stocks. A year ago, Mandaelo proposed a mathematical model for the stars in the universe (such as Kangto Dust).

Using this model can explain Obez's paradox without relying on the theory of Big Bang. However, this new distribution model has no name and suitable for it.

What does this statistical model look like? Some are similar to the phenomenon mentioned in the papers "Two Type Statistics" published by the Geographical and population scientist Jaromírkorˇcák in 1938. Mande Bero read his son's Latin Dictionary while meditation. Suddenly, a eye -catching Latin word jumped into his eyes: Fractus.

The interpretation of this vocabulary in the dictionary coincides with the idea of Mandaelo's mind: "separate, irregular fragments". Great, that is some separate, irregular, fragmented fragments! The term Fractal was born.

After that, Mandaelo also studied and described the collection of Mandaelo. He changed our worldview with the "beauty of fractal" found from the crushing. He is committed to introducing the theory of fractal to the public, so that the research results of the fractal are widely known. In 1993, Mandaelo, an academician of the American Academy of Sciences, won the Wolf Physics Award.

Mandael published the book "Flat Geometry of Nature" in 1975. This book laid the mathematical foundation for fractal theory and chaos theory. For Volkswagen readers, it is also a good book that recognizes it. There are a few words in the book: "The cloud is not just the sphere, the mountain is not just a cone, the coastline is not round, the bark is not so smooth, and the path of lightning spreads is not a straight line. What are they? They are simple and complex. 'Forming' ... "

Don't look at the "Father of Format" now, the phenomenon of scattered and broken phenomena he studied at the beginning is not a popular professional. Mandaelo often claims to be a "nomadic nation" in the academic world. He has been hiding in an unsustering mathematical corner for a long time, wandering in the narrow alleyway between the seemingly irrelevant orthodox disciplines, trying to find the rules from the crushing and discover the truth in empty concentration.

It is said that someone had scoffed at Mandaelo's work, thinking that he had just named it for the fractal. These so -called orthodox mathematicians laughed at the sky and said, "You can count what he can, you can't be a mathematician." Why? Because "most of his great works, you can't find a decent mathematical formula.

These self -learning experts have not figured out that those who lead any scientific development are always great thoughts rather than formulas, even if mathematics is the same. Later, the counter -examples quickly developed into a new discipline, and the stream gradually merged into the mainstream. Focus geometry and non -linear theory related to it affected each corner of science and society. Essence

The Chinese said, "The stone of other mountains can attack jade." Mandaelo used the small stone of the fractal geometry to knock on the jade about the difficulty of attacking in various disciplines. This can also be regarded as the biggest inspiration that the father of the fractal father has left us.

The well -known theoretical physicist John Waller commented on Mandaelo's work: "Today, if you don't understand the fractal, you cannot be regarded as a scientific and cultural person." Development will lead to new ideas, new ideas, and new applications, and new applications lead to new ideas ... "As if the fractal itself, the new ideas and new applications arising will be reciprocated, endless ... . In 2010, Mandalo died at the age of 85 due to pancreatic cancer. After his death, French President Sarkozy claimed that he had "a powerful and unique mind that was never scared by innovation."

"Devil's polymer"

The Mandaelo collection can be called the most strange and magnificent geometric figures made by human beings.

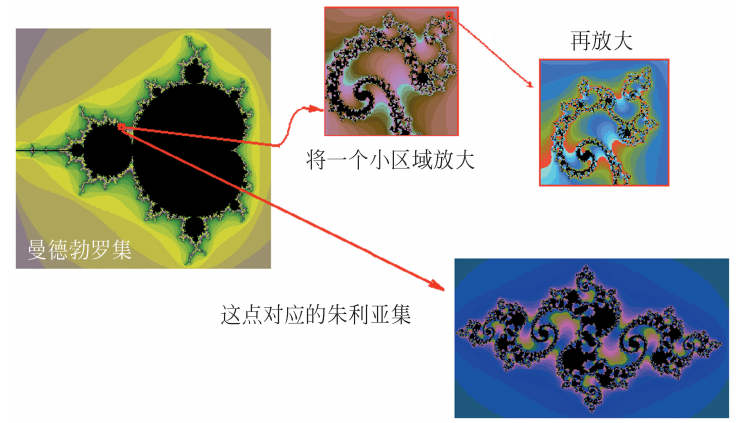
Figure 1 Graphs formed by the Mandajlo Collection

Zhang San was next to the computer in the library, and introduced the Mandaelo's computer program he wrote to his two friends.

Wang Er suddenly noticed that a girl was passing by. Wang Er knew that the girl's name was Lin Ling, and she was a freshman who was just enrolled. Wang Er's eyes tipped, and at a glance, she looked at a loose scarf on the girl's neck. With a movement in her heart, she walked over and talked: "Lin Zero, my name is Wang Er. Sorry, can you borrow your silk scarf? My friends see, its pattern is too similar to my friend's pattern generated by the computer just now! "

"Really?" Lin Zero was very curious, and followed Wang Er to the computer. Seeing that the picture called "Julia Collection" on the screen was indeed similar to the pattern on her scarf.

Figure 2 The silk scarf pattern designed by Mandaelo G Julia graphics (the graphic drawn from the red line is similar to the Julia set in the lower right of Figure 1)

At this time, several other students studying in the library also surrounded and appreciated the beautiful graphics that can be enlarged at will. No matter how many times the pattern is enlarged, it seems that there are always more complicated parts, the pattern structure is endless, some places are like a corona, and some places are like burning flames. The part of the magnification is different from the overall, and there are some similarities.

Someone said to Zhang San: "Wow, you are so amazing, draw such a complicated graphic, the program is difficult to write!"

But Zhang San said that it was surprising that this program was not difficult at all, and it was completed in a few hours. Because in fact, these beautiful and complex transformations are only from a very simple non -linear iteration formula:

What does this non -linear iteration mean? Li Si proposed Zhang San to briefly introduce the Mandael and his procedures on the blackboard at the table.

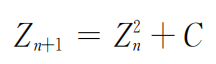
"Z and C in the formula are plural. We know that each plural can be represented by a point on the plane: for example, the X coordinate represents the real number part, and the y coordinate indicates the virtual number part. At the beginning, there are two on the plane. Fixed point: C and Z0, Z0 is the initial value of Z. For simplicity, we take Z0 = 0, so there are: z1 = c. We will express each position of each Z The original point is the highlight. After one iterative, the highlights move to C. After the formula, according to the formula, we can calculate Z2. It should be equal to C × C + C, and the highlights move to Z2. Calculate Z3, Z4, ..., keep counting. Like we use graphics in the previous sections as linear iterations. However, this iteration is required to be calculated, and it is not linear, so it is called non -linear iteration.

With the iteration of time and time, the position of the plural Z is constantly changing on the plane. We can imagine that starting from Z0, Z1, Z2, ..., ZK, highlights will jump around. Maybe it is difficult to see what the rules of its beating, but what we are interested in is that when the number of iterations K teles to infinite, where is the position of the highlights? To put it clearer, we are only interested in: When it is infinitely iterated, which one of the bright spots tends to be in two situations? Is it walking around in a limited range? Or will you jump to infinite far away? Because the initial value of Z is fixed at the origin, it is clear that the behavior of Z during infinite iteration depends on the value of the plural C.

In this way, we can get the definition of the Mandajolo collection: All the results that enable the unlimited iteration can maintain a collection of plural C. In Figure 1 generated by the computer, the point that is represented by black in the lower right is the Mandaelo collection. "

Li Si inserted in and explained a few words, about the "unlimited" mentioned by Zhang San: "It is impossible to make infinite many times when computers are iterating, so in fact, when K reaches a certain number, it is regarded as it is as it is as it is. It has been infinitely many times. Judging whether Z remains limited, the same is the same. When the distance from Z is more than a large number, even if it is infinitely far away. "

Wang Er and Lin Ling were sitting next to the computer, and they were amplified and enlarged by Mande Bero. Someone looked at Zhang San, who kept being magnified in the subtle part: "You just said that the black spots in the picture belong to the Mande Bollo collection, but I see these enlarged pictures, black spots and non -black spots Mixed together, there seems to be no clear boundaries in this Mandaelo collection. "

Li Si laughed: "The border of the Mande Plog has a surprising complex structure, and you can't see a clear boundary. It belongs to the point of Mandaelo's collection and the point of non -Mandaelo. Generally mixing together, you have me in you, I have you, and the black and white is not clear. This is exactly the characteristic of this shape ... "Another person asked," Then I have one more The question, if it is just a collection of Mandael and Mandael, the colors of black and white are enough. What's wrong with these colorful various colors? "

Zhang San explained how the various colors came from on the blackboard: "Don't we set different C values, Z started from 0? If after multiple iterations (such as 64 times) The distance D is less than 100. We think that this C value belongs to the Mandaelo collection, and the C -point C -point is black ... and other colors can indicate the different levels of the result of infinite iteration.

For example, the Z0 points of the last Z distance of the origin of the Z0 of the original point can be painted like this:

500> d> 100, C -point coating green;

10000> d> 500, C point C in blue;

1500> d> 10000, Point C is red;

D ＞ 1500, C point C is yellow ...

Doesn't this come out of the beautiful Mandaelo graphics in various colors? "

In order to make the students more convenient to study and appreciate the beauty of the Mandaelo collection, Zhang San gave him the website where he generated the program.

Julia's story

Wang Er enlarged the various areas of Mandaelo's collection, but he had not found the pattern similar to the forest scarf that Zhang San showed them at the beginning. Later, Lin Ling reminded him: "It seems that the picture is not called the Mandaelo collection, what is the Julia collection ..."

Figure 3 The left on the left is the Mande Bollo collection, and the right side is the Julia Collection corresponding to the Mande Berlot graphics (x = 0.379, y = 0.184)

What is the Julia collection?

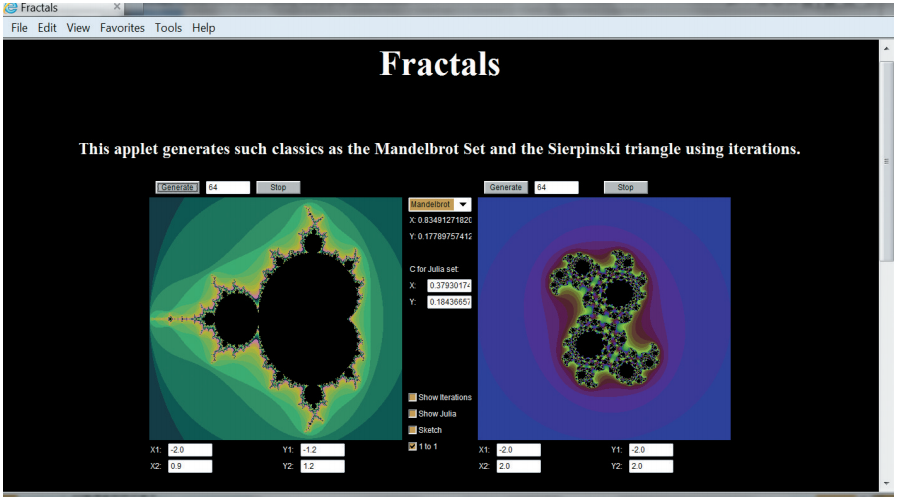
Li Si clicked on the Mandaelo graphics on the left of the screen with the mouse, and a beautiful graphic appeared immediately on the right side. Li Si told everyone that this is the Julia collection corresponding to the point of the mouse.

Then, he clicked in another position, and the figure on the right immediately changed. Every time the mouse changes, the graphic is changed.

In other words, every different point on the Mandaelo graphics corresponds to a different Julia collection. The Julia Collection and the Mandaelo collection are closely related. They are "relatives".

So, what is every point on the Mandajlo graphics? It represents different C values in the above iterative formula. Therefore, given a C, a Julia set can be generated. Indeed, the Julia collection is generated with the same non -linear iterative formula as the Mandaelo set:

The difference is that when the Mandajlo set is generated, the initial value of Z is fixed at the origin, and the different divergent of the track is identified by the different colors of C. When the Julia set is generated, we will fix the C value and use the initial initial Z's initial. The color of the value Z0 is to identify the different divergence of the track.

Although the names of Julia and Mandaelo are always connected, they are people of different times. Julia is a French mathematician (1893-1978) and 30 years in the morning than Mandaelo. Mandaelo did not died until 2010. Both of them lived to 85 years old, and Mande Bollo was known as the father of fractal and became widely known. However, as early as Mandaelo was born, Julia had studied in detail the iterative nature of the general rational function Julia.

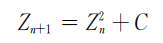
Julia

Julia's life is half -hearted, especially in your youth. He was born in Algeria. When he first entered elementary school at the age of 8, he entered the fifth grade and soon became the best student in the class. Later, 18 -year -old Julia won scholarships in Paris to study mathematics. But life is not very smooth for this young man, especially later, France rolled into the First World War. 21 -year -old Julia participated in a battle. Nose.

He has not been able to repair Julia's face many times, so he has been hanging a leather case on his face. Later, he studied mathematics with tenacious perseverance and completed his doctoral dissertation in the hospital for several years.

1918 was a year of good luck after the Julia disaster ended. This year, he was 25 years old and published a masterpiece of the 199 pages of 199 pages in Pure Mathematics and Applied Mathematics Magazine, so he became famous.

Although Julia has contributed in many areas of mathematics, it has left nearly two hundred papers and more than 30 books for the world in terms of geometric analysis theory. The name is noisy.

But unfortunately, after a few years, the work of this iterative function seems to be completely forgotten. Until the 1970s and 1980s, the foundation geometry laid by Mandaelo and the concept of chaos related to it were extensive. After being applied to various fields, Julia's name spread with Mandaelo's name. Such things are common in the history of mathematics and physics, just like Riemann geometry is familiar with everyone because of the general theory of relativity.

It can be seen from the generation process of the Julia collection: there is a Julia collection corresponding to every point that is concentrated in Mandaelo. For example, click the zero point on the Mandajlo set (the corresponding C value is 0). At this time, the Julia set generated by the above iterative iteration is a unit circle. Figure 4 shows different Julia sets (8 small pictures around). They correspond to different points in the Mandajlo set (big picture in the middle).

In summary, we understand the process of the Mandajlo set and the Giolia collection graphics. The shape of this non -linear iteration method is not only loved by the artists by its mysterious complexity and changing versatile. development of. So that people praise the latter as the third revolution in science comparable to relativity and quantum mechanics in the 20th century.

In the 1990s, academic circles, including science and technology, art, society, humanities,, in almost every field, there were fractal research: stock market experts looked for self -similarities in the huge data of the market. Whether the melody created by the rules is more mysterious.

As a Western saying says: "In the view of the carpenter, the moon is also made of wood." Everyone understands the world in their own way. Various majors may be very different about the fractal, but the enthusiasm for this new type of science is consistent.

Book Author: Zhang Tianrong

Part of the article source network

Edit: Zhang Runxin

Reprinted content only represents the author's point of view

Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences

If you need to reprint, please contact the original public account