Hey, dogs and insects, hehe!

All of this originated from the Ke pig lying in the storage room today, like a large piece of bread.

It used to shrink his feet habitually, and it seemed like a dog worm without your feet at a glance. It seems that many dogs like to turn into dogs and insects, because they are often pretending to be poor and can't help but sigh that they are really poor dogs ... Bushi.

Of course, dogs and insects are really cute. Corgi can become dogs and insects to the greatest extent because its chassis is too low and most of the body (fat) wide (like) body (like) strong (pig). If it is a long -legged German shepherd, it will become a dog and insects. "Divine Gong" will shrink bone power afterwards.

Zhang Wuji: Do you think you are humorous?

In fact, the only difference between dogs and dogs and insects is that dogs have four legs. If you remove the dog's four legs, or just remove the four leg bones, and then stretch the relaxed skin and stretch, the dogs and insects will be completely born.

For specific images, you can refer to the close relative bread dogs and sausage dogs of the dog insects

Some people may ask, why do you have no flesh with a lot of bones? Just now, this so -called "stretching" is the key to stretch the relaxed skin. In other words, in fact, as long as you do n’t have a hole in your body, the dog insect does not care what the shape it becomes. The only thing about dogs and insects cares about whether it is complete. If you still can't understand this process, you may wish to look at the picture below.

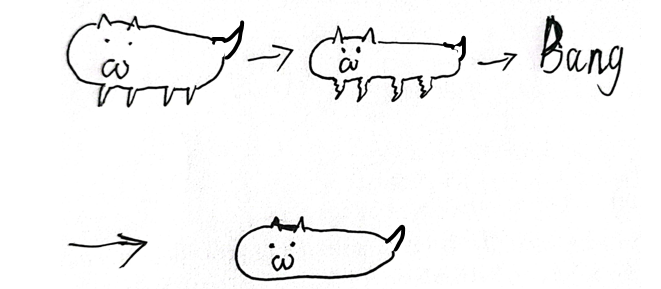
Remove bones, stretch, bang, magic allowed dogs and insects to be born (Jiuzhen Painting)

So we can get a characteristic of the dog insects: dogs and insects do not care how long their legs are, and it only cares about whether its round body is damaged. If dogs and insects can be more "freely and free", such as "stretching" with mouth and tail, then it can become a boring orange with ears.

Soul painting skills

If we strictly the changes in dogs and insects, we can get the nature of one type of operation: do not care about the specific distance between the various parts in the process of continuous changes, but only care about the positions of each part and the overall overall as a whole In other words, what is concerned about continuous changes. After all, you did not make a hole in the dogs, and you did not let the dog's face upside down.

What often reverses other people's faces is generally called Picasso

In fact, in addition to dogs and insects, people have done many other changes in the sky. The most famous is an example of a coffee cup.

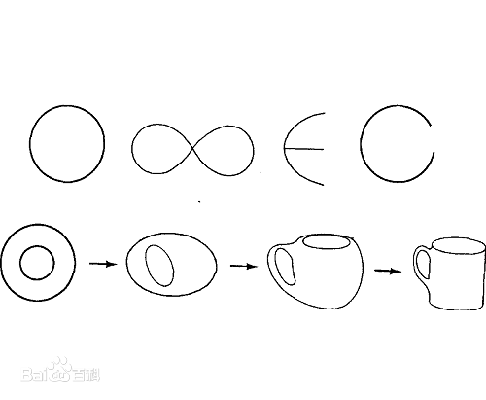
Whether it is dogs and dogs, or donuts and coffee cups, there is a term to describe the relationship between them: topology equivalent. You must have heard the word "topology", at least you should have heard of the famous story "Kenisburg Seven Bridge Questions" related to topology.

Konisburg is now Kaliningrad in Russia.

Euler's work on this area can be considered as the beginning of topology. Of course, strictly speaking, the concept of topological space is required to study topology. The definition of topological space is listed as follows (it doesn't matter if you don't understand):

Let X is a collection, o is a family composed of some subsets, then (x, o) is called a topology space. If there is:

1. The empty set and X belong to O,

2. Multi -elements of any elements still belong to O.

3. The intersection of the limited elements still belongs to O.

The elements in X are called points, and the elements in O are called opening. Also known as O is a topology on X.

As for what is the topology equivalent, it can give a definition in a less strict but more intuitive language, that is, there are several graphics. If each one can be twisted, curved, stretched or contracted from any other graphics, it can be obtained by the other one. Without any overlapping and disconnection, these graphic topology equivalent is called topology transformation. The main point of this transformation is that the nature of the graphic cannot be changed. For example, the smooth curved surface cannot be changed into the corners, nor can it be a hole in the surface without holes. So even if it is a whole, the Slime of MineCraft and the Slime of "Tyraria" cannot be a family -after all, there is essential differences between the square and the shed.

Mung bean cake and red bean dumplings (bushi)

When changing, the topology graphics has the same nature. For example, the number of donut holes is a nature. If a graphic looks complicated, but if you only study these unchanged properties, we can make it simply to make it simpler, or consistent with the graphics we know. So in the field of classic physics, what shape is the most complicated? According to Einstein's idea, it is naturally the universe. (Manual dog head)

Of course it is not ruled out that Lu Xun said

The problem of the universe is that it is too big to have no edges. The general theory of old love said that the universe is a pseudo -Riemann form, and the partial equivalent of Mincofoski is equivalent to the time and space. However, even if the goose is Mincofsky's time and space, it is too great to grasp it. However, it is well known that the water for selling wine is too deep, Gazi can't hold it, but Uncle Pan can. There are also people who can grasp the universe, that is Roger Pairos.

Roger Penrose (1931.8.8-), British mathematical physicist, won the Nobel Prize in 2020.

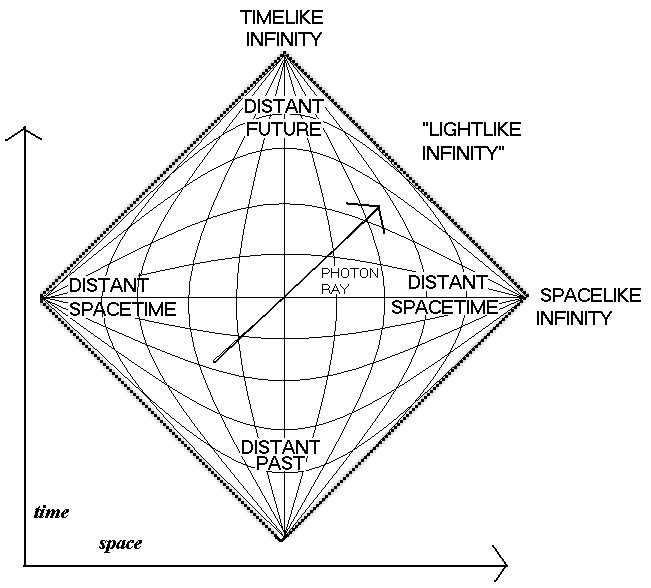
In order to facilitate the study of the overall time and space topology, Penrus introduced the famous Penrust, and still maintains the causality before the transformation after the transformation -just a little hand and feet before the transformation, that is, under the coordinate transformation, the coordinate transformation Perform the maximum analysis Yan Tuo. As for what is a parsing extension, it is simply a function that the corresponding expansion function needs to be smooth and continuous after the expansion of the definition domain. It can be proved that the parsing Yan Tuo exists and is unique. Mincofoski time and space are relatively simple, and there is no need to analyze Yan Tuo. Getting the goal surface: a specific coordinate transformation:

Can be written as:

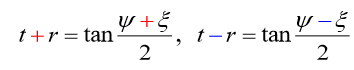
Because the actual parameter R does not get the negative value, time and space can only be part of the new coordinate system, so its Penrust is like this:

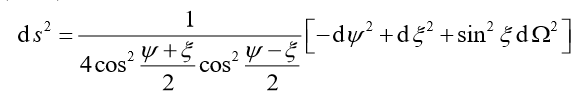
The boundary and intersection of Pengrust in Mincofski time and space represent the infinity of different meanings (the boundary of R = 0 is an exception). Because the transformation adopts a common transformation -co -shape transformation is not a topology transformation, but in Peng The two in Rostu -these borders and intersections are also called "unpinity and far away." In fact, because infinite and far away represents a trend and not specific value, infinity is not inside the space -time. These boundaries and intersection points cannot be regarded as part of Peroastu, so that it can be considered the topology. After the transformation, the cause and effect were retained, and the ground -metering line was still the ground test after the re -selection of the parameters. Because a two -dimensional plane map certainly does not reflect a four -dimensional space -time, every point in Pairus is actually a two -dimensional spherical.

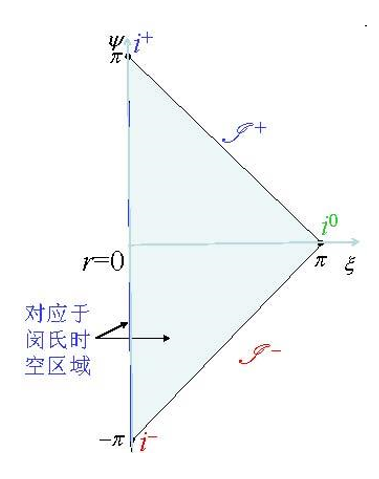
In fact, Pengrust, who is in time and space of Mincofoski, can continue to be extended into the picture above, but the time and space after Yan Tuo is called Einstein's static universe, which is different from the topology of Mincofoski time and space.

Then someone wants to ask, ah, this is the straight time and space of Mincofoski, what should I do if the curved Riemann time and space do? It is better to look at a famous example: Swarie Time and Space.

Karl Starcas and Starisis solve, the solution describes a static, inductive, and symmetrical gravitational field outside the celestial body.

First of all, through some strange coordinate transformations (the process is too complicated, it will not be released), we also transform from the ball to a new degree:

This degree is called Cruzcar's gauge, and coordinates T and R are called Crusscar coordinates. The maximum extension means that both T and R parameters can get the entire real set. In fact, due to the existence of strange points R = 0 and infinite far away, the time and space after Yan Tuo is only part of the Cruzcar coordinate system. On this basis, Puerustu can also be drawn after time and space Yan Tuo.

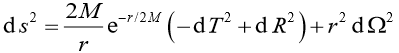
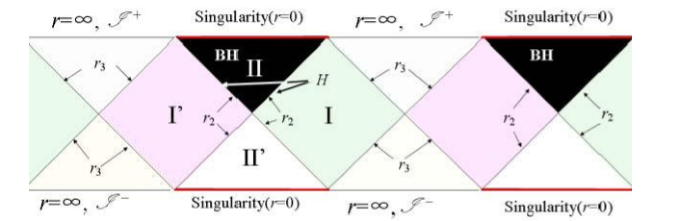
The largest extension of Starcas (left) and Puerosetu in the Crusscar coordinate

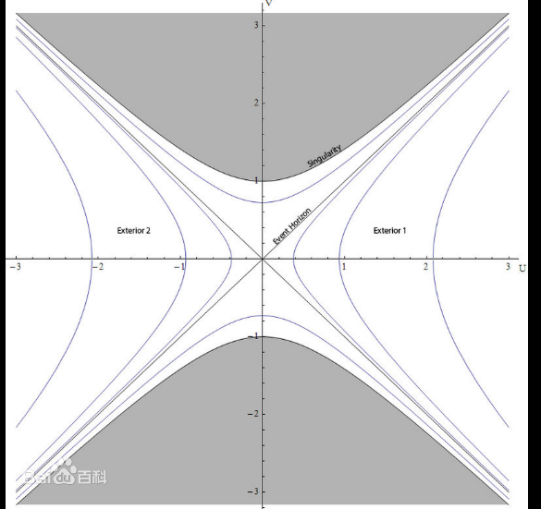
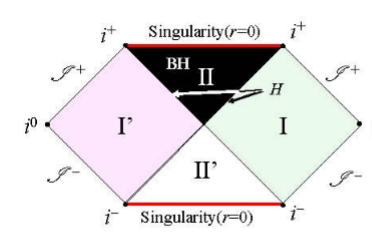
Area Ⅰ in Perowlus is the primitive space -time area (outside the black hole), and the Ⅰ 'area is the time countermeasure area. The Ⅱ and Ⅱ 'are called black hole and white cave area, respectively. The middle connection point in the middle is called "throat", and it is also called wormhole (that is, the wormhole often mentioned by the marketing number).

I have heard you have heard of worms countless times, but I should not expect that this thing can appear here.

In this way, through the change of topology, a large and large space -time is limited to a hexagonal shape. The cause and effect of time and space are still retained. The evolution trend. Even for more complicated time and space, such as Swadas-Anti-Destet time and space, Kle time and space, etc., Penrusto can still greatly simplify the image of time and space-because the maximum extension of Kerl is very difficult to draw itself — And describing the time and space itself well, I have to say that it is a very powerful tool.

From top to bottom: Schwarzschild- (Anti-) de Sitter, Penrust, Reissner-Nordström in different time and space in Pueros Tu, Kerr-Jeuman (Kerr-Neuman) Pengrustu under different conditions of time and space

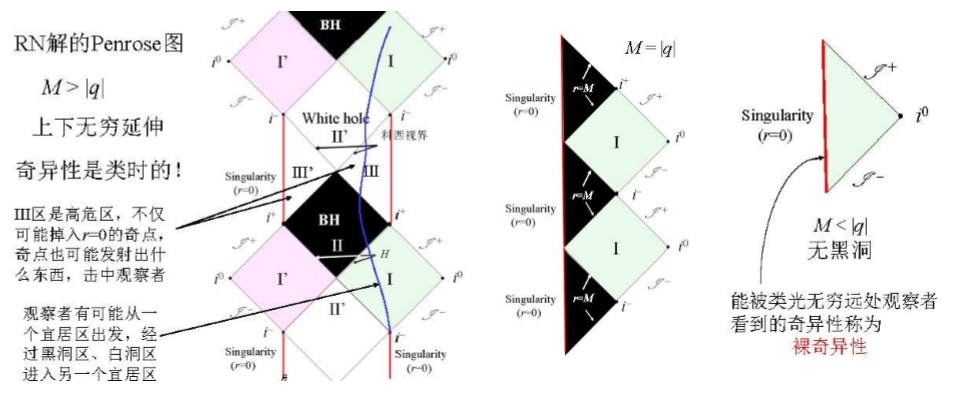
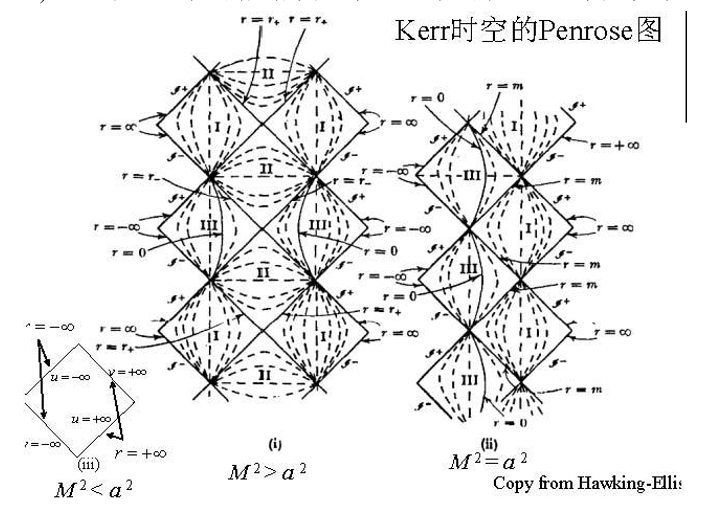
Of course, Penrust is just a small application in physics in physics. In addition, there are topology in the theory of condensation, and there are topology field theory in quantum field theory. You can imagine that topology research physics must be extremely powerful tools.

PS: Pay attention to the weight of dogs. Our family has begun to exercise. Don't urge it ~~~

*: According to Teacher Liang Canbin, there is infinite and unprepared point as part of Penrust. There are also some teachers, such as Teacher Huang Chaoguang of Gao Energy, which regards it as part of Peerust, so you need to remove it when discussing the nature of the topology.

Reference materials:

[1] (US) James · R · Munkres. Topology [M]. Second edition. Machinery Industry Press, 2004.

[2] Huang Chaoguang. Lecturer of the general theory of relativity.

[3] Robert · m · Wald. General Relativity [M]. The first edition. The University of Chicago Press, 1984.

edit:

- END -