How did the magician know the numbers in your mind?

Read the following articles carefully, and think about the questions raised at the end of the article, and strictly follow the interaction: leave a message in the comment area in the comment area, you will have the opportunity to get the high -quality popular science books provided by China Industrial Information Publishing Group and People's Post and Telecommunications Publishing House. A copy of the Weather Book Exploring the Weather "

Mathematics magic is like reading technique. You need to reveal the secret behind the following tricks.

Mathematics follows certain logic. If a situation can be accurately described with mathematics, sometimes it is possible to predict what will happen in the future in advance -for example, the time of lunar eclipse. For those who are unfamiliar with prediction, this result looks like magic. In fact, Arthur CLARKE, a science fiction writer, said: "Any advanced technology is no different from magic."

In today's "mystery of insights", we will explore four examples of mathematical magic. At first glance, they seem to be read. Just like stage magic, these examples will make you think: "How do they know what I am thinking?"

Most of us had such experience when we were young. A friend made us think of a figure, but don't say it. Then perform a series of simple arithmetic operations on this number. Finally, friends will gently say the secret number that we know only, how surprising! How did this do?

A simple example here may surprise the children around you and even inspire his interest in mathematics. Lewis Carroll, the author of "Alice Dreams", used it for this purpose. Corol is an Oxford mathematician and a puzzle who loves puzzles. Many mathematicians are very interested in his puzzles, including the famous Tereste Tao.

Puzzle 1

This magic is suitable for children who can be counted as a multiplication (if not, you can find someone to help). Let Xiaohong (or Xiaoming) think of a three -digit number, but don't say it, tell them that you can change two secret numbers. The first step is to let Xiaohong take the number 7, then multiply 11, and finally, add appropriate magic performance and language, and then take the result to 13.

If she is right, she may find that she laughed happily. And for you, or for a bigger child, the question is -how to do it?

Click here to get the answer

Smart readers have discovered that this process is to multiply the secret number by 7 × 11 × 13 = 1,001. This number can "copy two copies" of the original three -digit number, such as the secret number is 457:

If you are interested in more mathematical problems of Lewis Corol, you can find more here. Let us enter the more difficult puzzle now.

Puzzle 2

There are two unknown numbers between 2 and 9. This number can contain 2 or 9, or the same. S and P are two mathematicians with clear logic. S knows the sum of the two numbers, and P knows the accumulation of two numbers. Then their conversation is as follows:

S: I can't infer what these two numbers are.

P: I can't infer what it is.

S: Oh, then I know what it is!

P: Then I know too!

At first glance, this seems to be a magical reading technique -where do they get new information to solve the problem? Can you find these two numbers (there are two possible answers), can you explain how S and P do it?

Tip: All possible situations of s and p are made into forms to find information that can be inferred in the dialogue (remember to consider the possible situation). This does not involve any difficult calculations, but it is easy to confuse their respective information.

Click here to get the answer

Here is an analysis: Draw a 8 × 8 table according to possible situations, the element (and, accumulation) of the form of the form, analyze the possible numbers based on the dialogue between the two:

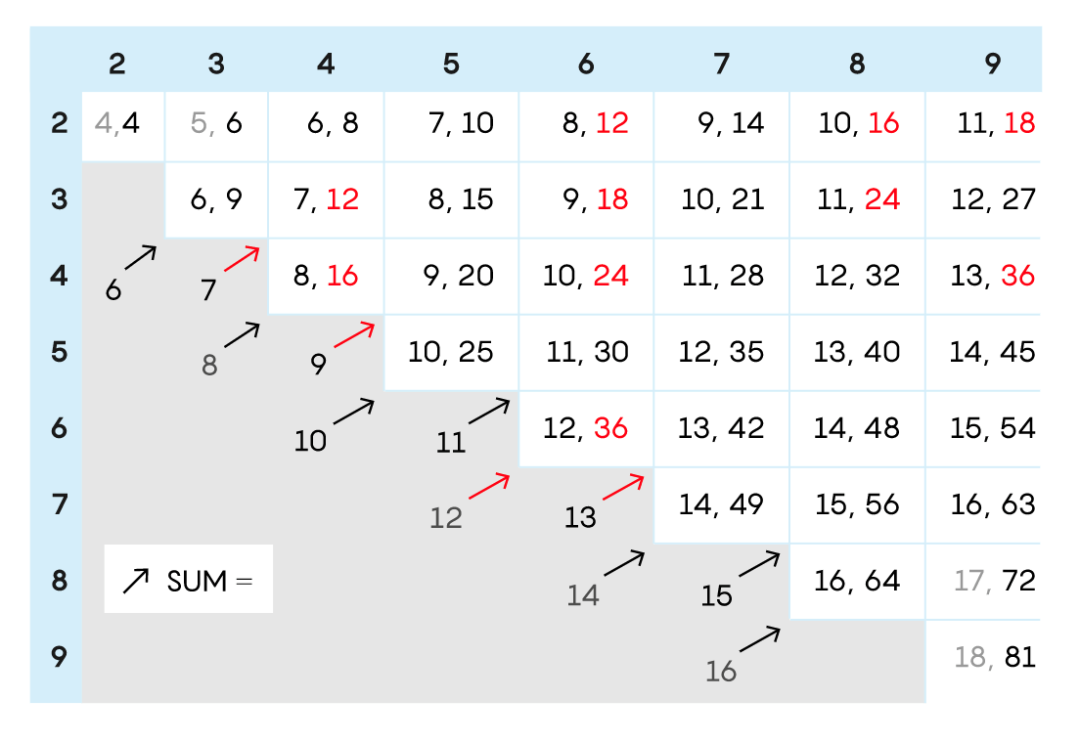
1. S说他无法推断出这些数字是什么时，意思是，他得到的和在表格中不止一次出现，去掉那些只出现一次的数字：4（2+2）、5（2+3）、 17 (8+9) and 18 (9+9), these can be deleted from the list and displayed as gray in the figure.

2.同理，P 说他也不能推导出这些数字，说明他得到的乘积也不止出现了一次，找到出现不止一次的数字：12（2×6，3×4）、16（2×8， 4 × 4), 18 (2 × 9, 3 × 6), 24 (3 × 8, 4 × 6), and 36 (4 × 9, 6 × 6). These results are displayed in red, and others may be eliminated.

3.S can derive the product. This means that only one of his numbers in these pensions are possible. Therefore, we need to observe each diagonal line, and choose the diagonal with only one red product. The possible situations are: 12, 18, 36, and 36, and the corresponding and the following are 7, 9, 12, and 13 respectively (shown in red arrows).

4.P can derive peace, which means that only one corresponds to his product. 36 can be excluded, because the total of 36 may be 12 or 13. Therefore, the only optional Hyebile pairs are (7, 12) and (9, 18), which correspond to the original number pairs (3, 4) and (3, 6). The answers (3, 4) and (3, 6) are in line with the problem statement, and they are correct. However, reader Demin said there was only one correct answer (3, 4). It can be seen in the next puzzle that as the optional number limit increases, the answer to this kind of puzzle may change. If the range of numbers changes from 9 to 10, then (3, 4) is still a solution, but (3, 6) It is not, so (3, 4) is regarded as a stable solution to the original problem. Like (3, 6), the solution that appears and disappears when changing the digital range. Phantom solutions).

The following is a more difficult version, which has more possibilities.

Puzzle 3

Now, there are two numbers (can be equal), now they are between 2 and 70. Similarly, give S two sums of numbers, and give p to the accumulation of two numbers. Their dialogue is as follows

P: I can't infer what these two numbers are.

S: I can tell you, although I can't infer the number.

P: Oh, now I know what these two numbers are!

S: Me too!

Find what these two numbers are, how S and P are calculated.

Among the puzzle 2, there are 15 different and 64 different pilots. Of the puzzle 3, 137 and 4761 areas.

Through the list method, you can find the solution of puzzle 2, but to the puzzle 3, you can try to use electronic tables or programming to calculate. Some readers will undoubtedly do this. But if you think about the first sentence of S, you can use some ideas of the initial number theory to limit some possibilities to solve this problem on paper. So the second question is: how many cases are the minimum possible manual calculation after excluding some options?

Click here to get the answer

Here is the solution to the reference:

1. Because P cannot derive two numbers, P cannot be the product of the two prime numbers. Similarly, S is not the sum of the two prime numbers. There is a Gota Bach conjecture here, which may be the most famous conjecture that has not been confirmed in the number theory. Gothic Bach conjecture pointed out: The even number of Ren 1 can be expressed as the sum of the two prime numbers. Although this conjecture has not been proven, the even number below 4 × 1018 is established. Because the range we guess is far less than this, we can say that S cannot be even.

2. On the other hand of derivation 1, I call it derivative 2: S cannot be the sum of the prime numbers and 2, because 2 is a prime number. For example, S cannot be 9, because 9 is the sum of prime numbers 7 and 2, and their multiplication is 14, only one decomposition: 2 × 7. In this case, P will immediately know what these two numbers are.

3. Finally, S must be less than or equal to 2 plus a prime number. This prime number is the minimum number of the minimum element greater than half of the limit. For example, when the range is 70, the number of prime is greater than 70, that is, the minimum number of 35: 37. According to the rules, S cannot be greater than equal to 39. This condition is limited by the range of the product. For example, if S is 39 and 37+2, it is all prime numbers, which will be inferred immediately and not satisfied with derivation 2. The next odd number is 41, its multiplier is 37 × 4 = 148, and it is decomposed to 74 × 2, 74 exceeds the range; the other may also be inferred by two numbers that decompose 37 × 4. In the same way, 37+6, 37+8, 37+10 ... until 70. Generally speaking, any odd number of greater than 39 can be expressed as 37+x, where X is even, so such a factor can be decomposed into a 37 × x form.

4. According to the above derivation, the possible number of possible numbers can be reduced to 11, 17, 27, 29, 35, and 37 with the first three dialogues of S and P. This is great, but it can be further. The key to the fourth sentence of S is: there must be a unique pilot p corresponding to S. Looking at the situation of S = 11, it can be expressed as 3+8 or 3+23 may also be 7+4 or 7+22. If P derives S is 11, then P may be 24 and decompose to 3 × 8. S is 11; another situation of decomposition of 2 × 12 is given S to 14, and it is not established according to derivative 1; the situation of 4 × 6 is 10, which is also excluded. If P is 28, decompose to 4 × 7, S is also 11, allows; decompose to 2 × 14, S is 16, not allowed. Therefore, in the case of a given S to 11, it is impossible to determine whether P is 24 or 28, so it is given here: S cannot be represented by Y+2n, where Y is a strange number.

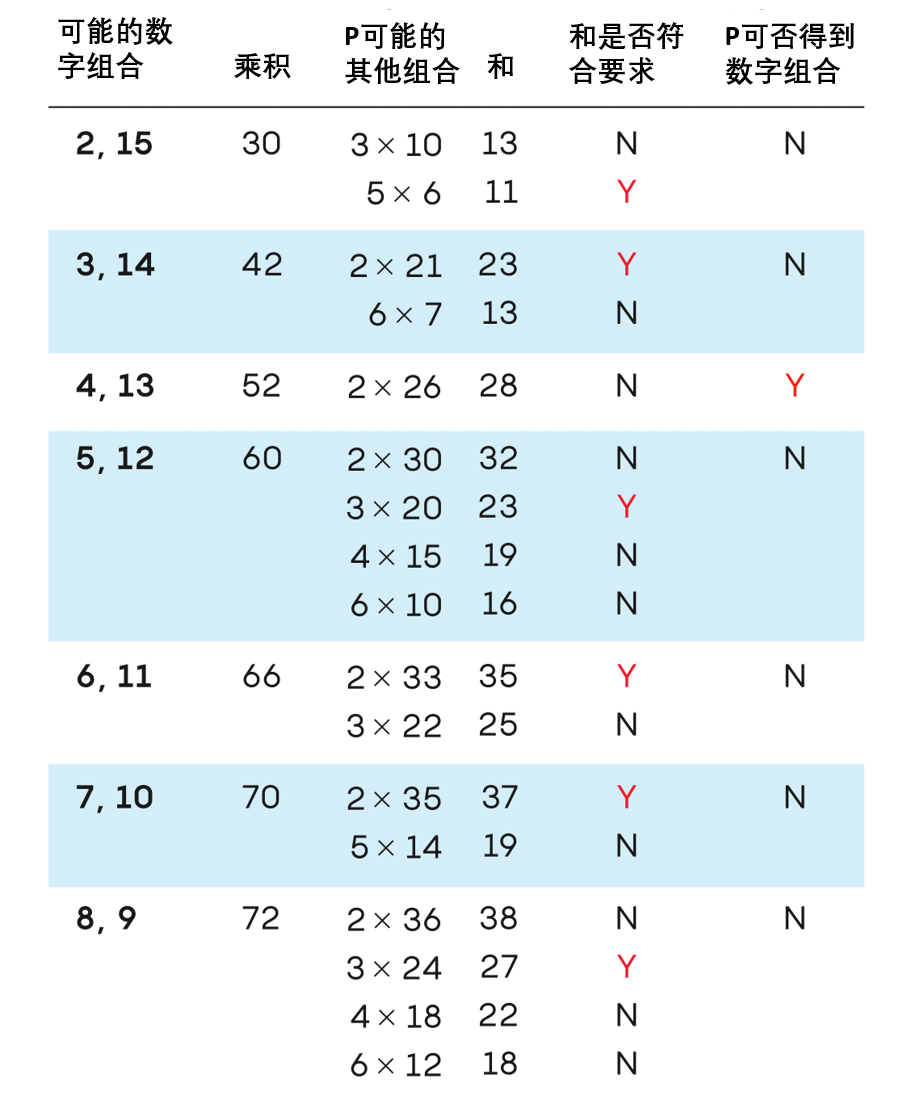
From the current candidate figures, 11 has been excluded. Similarly, 23 (19 + 4 and 7 + 16), 27 (23 + 4, 19 + 8 and 11 + 16), 35 (31 + 4, 19 + 16, 3 + 32) and 37 (29 + 8 and 5 + 32) was also excluded. There are only 17 and 29 possibilities left now. The options of 29 can be excluded, because 13+16, 25+4 are possible, and there must be only one option according to the dialogue S. The possible situation of S = 17 is given in the table below. The first column has a pair of candidate numbers, the second column corresponds to its product, and the third column is a possible number given for the product. What is harmonious. The fifth column represents these and whether the dialogue is allowed (one of the 11, 17, 23, 27, 29, 35, and 37). Even the Y obtained by the fifth column does not mean that P knows these two numbers, because the pair of the first column may have two numbers pairs. Combined with the sixth column, there is only one possibility, that is, 4 × 13, which is the only answer of the puzzle.

The next question shows how to show my mind in the card drama. But this trick is strict mathematical skills, and there are some interesting mathematical principles behind it.

Puzzle 4

A "Mathematical Master" threw away the number of 2 to 6 in the card, thereby preparing a pair of 32 cards. He arranged the remaining cards in a certain order, and then placed on the table. Randomly select five people to sit next to the table, and then cut the card one by one. Then the first person took the top card and passed the card group to the second person. When everyone has a card, the last person puts the cards down on the table, and then returns to his seat.

Now, the performers are required to teleport the card to him in an inspiration. He frowned concentrate, and finally shook his head helplessly. "It is getting more and more difficult these days. The expansion of the universe has caused red shifts, which interferes with the color I received. Would you please stand up with a red card?"

The second and fifth participants stood up. The mathematician's face passed a hint of comfort. "It's clear now, you have a red heart 10, you have block K." The fact is indeed the case, he also guessed the cards of the other three people.

How did he do that? Well, since I told you that this trick is a strict mathematical skills, it is clear that he remembers the order of the card (maybe a certain code may be used), and the card order is saved in five random cuts, you know why ?

Tip: Considering the sequence 00010111, it periodically includes eight possible three -combined number of 0 and 1: 000, 001, 010, 101, 011, 111, 110, and 100. What will happen if you "cut" it like a poker card?

Is the performer's interest on the stage pure teasing or the key to play? When you play this trick, can you come up with the order of cards?

Click here to get the answer

Here is a solution provided by a reader.

The sequence 00010111 is called the 3 -level de subt sequence on 0 and 1. It is equivalent to cyclically a cycle like a poker card. At the same time, it still retains the attributes of its sequence. We can construct all possible sequences composed of 5 and R, for example:

BBBBBBBBBBBRBRBRBRBRRBRBRBRBRRRR,

Its length is: 25 = 32 bits, which is the same as our card number, letting each B in the sequence in the sequence corresponds to a black card and R corresponds to a red card. Each of B and R is unique, so once you know where the red is, you will know the entire order of the five cards (BRBBR). Then simply remember the order of the card until you find the order of the corresponding five cards, you know the answer. In the performance, in order to find the order of the red card, the joke process is necessary.

I hope you can infer more information from the various information in the above puzzles. This is the mystery of magic! Enjoy the fun of solving these magic!

Author: Pradeep Mutalik

Bleak

Translation: NUOR

Review: zhenni

Original link:

https://www.quantamagazine.org/how-do-math-magiCians-know-Y-Number-20220504/‍

https://www.quantamagazine.org/the-secret-math-mind-reading-Magic-tricks -20220527/#Comments

FU

blessing

li

profit

shi

Time

jian

between

Today we will send out the "The Mystery of the Weather Book for Children" provided by China Industry Credit Publishing Group and People's Posts and Telecommunications Publishing House.

This book is a popular science book about the mysteries of weather. The book is divided into three parts. It tells the various weather phenomena and meteorological disasters in life.This book cuts from typical weather phenomena, such as wind, cloud, rain, snow, fog, etc., reveals the principles behind various weather phenomena in daily life. There are many interesting experiments in the book. Readers can do it by themselves to do one by one.Do.The content of this book is derived from the weather.It is a very suitable weather science enlightenment book for children.Interactive question: What do you know "tricks" with mathematical or physical principles?

Please strictly follow the interaction: the format of the question answer is

In order to ensure that more friends can participate in the award, friends who have won the award in the past four periods cannot receive prizes, and the ranking will be postponed in order

*This event is limited to the WeChat platform

Translation content only represents the author's point of view

Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences

Edit: zhenni

- END -