Is the chance of winning a lottery to win the lottery than ordinary people?

Today, the term "probability" can be seen everywhere in our lives, and people are more and more widely used. Because this is a more and more changing world: everything is changing, everything is difficult to determine. Our world can be said to be composed of variables, including many decisive variables. For example, the news said: "At 20:43 on November 3, 2016, Beijing time, the Long March 5 was successfully launched in Wenchang, Hainan." The time and place here are determined decisive variables.

However, there are also many random variables that are difficult to determine in our lives, such as the extent of the haze tomorrow, or the stock value of a company, and so on, all are uncertain random variables.

Random variables are not expressed in fixed numerical values, but described by the probability of a certain value. Because there are random variables everywhere, the term "probability" is heard everywhere. You turn on the TV to hear the weather forecast and see if it will rain today. The meteorological forecastr told you: The "precipitation probability" at 8 o'clock this morning is 90%; you go to the mobile phone to check some kinds of stocks in the stock market, you you, you, you得到的信息可能是这种股票3个月之后翻倍的概率是67%；你满怀期望地买了50张彩票，朋友却告诉你，傻瓜才去白花这50块钱，因为你中奖的概率只有One hundred million ...

Picture source: PEXLS

The word "probability" in life is too common, so that people do not think about what it means. For example, in the last example, the meaning of vicious probability of 0.03%is not to say, "10,000 of such sarcoma. Is it only three of them "? Therefore, in the classic sense, the probability can be roughly defined as the frequency of the event, that is, the ratio of the number of times to the total number of times. More precisely, the total number of times is infinite, and the limit of this ratio is approaching.

Picture source: PEXLS

Although the definition of "probability" is not difficult to understand, it seems that everyone uses it, but you may not know that the results of probability calculations often violate our intuition. There are many impossible explanations and specious paradoxes in probability theory. Can't fully believe in intuition! Our brain will have misunderstandings and blind spots, just like there are "blind spots" in the driver driving in the car. It takes a few mirrors to overcome. There are also blind spots in our thinking process. We need to clarify by calculation and thinking. Probability theory is a strange conclusion that is often contrary to intuition, and even mathematicians will be mistaken for a little carelessness. Now, we first give an example of a paradox in the classic probability, called "Base Rate Fallacy".

We start from an example in life.

Wang Hong went to the hospital for a test to check the possibility of suffering from a certain disease. The result was actually positive. He was frightened and hurriedly checked online. Online information says that there are always errors for inspections, and this test has "1%pseudo -positive rate and 1%pseudo -negative rate."

The meaning of this sentence is that 1%of the people who are sick are fake negative and 99%of them are true positive. In the inspection of people who did not get sick, 1%of people were false positive, and 99%of them were really negative. Therefore, based on this explanation, it is estimated that he had the possibility of the disease (that is, the probability) of 99%. Wang Hong thought that since only 1%of the false positive rate, 99%are true positive, then the probability of this disease in the crowd should be 99%.

However, the doctor told him that the probability of being infected in ordinary people was only about 0.09 (9%). What's going on? Where is Wang Hong's misunderstanding?

Picture source: PEXLS

The doctor said: "99%? How can there be such a large probability of infection. 99%is the accuracy of the test, not the probability of your illness. You forgot one thing: the normal proportion of this disease is not large, Only one of the 1,000 people is sick. "

It turned out that the doctor also liked to study mathematics, and often used the probability method for medicine.

His calculation method is basically the case: because the test misunderstanding rate is 1%, 10 people will be reported as "false positive", and according to the proportion of this disease in the population (1/1000 = 0.1 0.1 %), There is only one true positive, so about 11 tests of the positive person are true positive (disease). Therefore, the probability of Wang Hong's infection is about 1/11, that is, 0.09 (9%9%(9%(9% To.

Wang Hongsi still felt confused, but this incident inspired Wang Hong to revisit the probability theory he learned before. After reading repeatedly, after thinking about the algorithm of the doctor, he understood that he had committed the mistake called "basic ratio fallacy", that is, forgetting the use of "the basic ratio of this disease in the population (1/1000)" fact.

When it comes to the basic ratio fallacy, we better start with the famous Bayesian theorem in probability theorem.

Thomas Bayes (1701-1761) is a British statistician and was once a priest. Bayesian theorem is his biggest contribution to probability theory and statistics. It is the basic framework of machine learning commonly used in artificial intelligence today. Instead of understanding this. Because of such an important result, he did not publish it during his lifetime, and was published by a friend in 1763 after his death. Roughly speaking, Bayesian theorem involves the interaction of two random variables A and B. If a sentence is summarized, this theorem says: how to modify the new information brought by B, how to modify B when there is no existence of B, A does not exist, A does not exist. "Priority probability" p (a), so as to obtain the "conditional probability" p (a | b) when the existence of B, or the postponement probability, if it is written as a formula:

The definition of priority and post -inspection here is a convention, which is relative. For example, A and B can also be described in turn, that is, how to get the "conditional probability" p (b | a) from the prior probability p (b) of B, see the dotted line referred to in the figure.

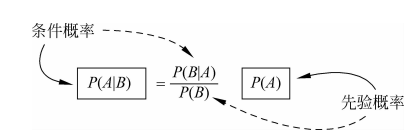
Don't be afraid of the formula, we can understand it slowly through examples.

For example, for the example of Wang Hong to see a doctor in front, random variable A represents "Wang Hong has some kind of disease"; random variable B represents "Wang Hong's test results". Priority probability P (a) refers to Wang Hong's probability of this disease when the result of no examination (that is, the basic probability of this disease in the public is 0.1%); and the conditional probability (or post -test probability) P (a A) P (a A) | B) Refers to the probability of this disease (9%) under the condition of Wang Hong's "test result is positive". How to modify the probability from basic probability? We will explain later.

The Bayesian theorem was the product of the 18th century. It was used well in the last 200 years, but did not want to encounter challenges in the 1970s. The challenge came from Daniel Kahneman and Tersky. "Basic ratio fallacy". The former is an American psychologist in Israel, the Nobel Prize winner in 2002. The basic ratio fallacy is not to negate Bayesian theorem, but to explore a question that makes people confused: Why does human intuition often violate the calculation results of the Bayesian formula? As the examples just shown, people often ignore the basic probability when using intuition.

Canman and others held an example of a taxi in their article "Thinking, Fast and Slow" to inspire people to think about this reason that affects people's "decision -making". We don't want to talk about the meaning of the basic ratio of the "decision theory" here, but we only use this example to deepen the understanding of the Bayesian formula.

If a city has two colors of taxis: blue and green (the market share is 15: 85). A taxi escaped after an accident at night, but fortunately, there was a witness at the time that the witness found that the taxi was blue. But what is his "witness"? Public security personnel performed the "blue and green" test on the witnesses in the same environment: 80%of the identification is correct, and the situation of 20%is incorrect. Maybe some readers immediately concluded that the probability of the accident of the accident should be 80%. If you answer this answer, you will make the same mistake as Wang Hong in the above example, ignore the priority probability, and do not consider the basic proportion of the "blue -green" car in this city.

Picture source: PEXLS

So, what should the probability of the accident of the accident should be blue (condition)?

The Bayesian formula can give the correct answer. First of all, we must consider the basic ratio of blue -green taxis (15: 85). In other words, in the absence of witnesses, the probability of the accident is only 15%. This is the prior probability p (a) = 15%of the "a = blue car accident". Now, with a witnesses, the probability of incident A appears. Witnesses see that the car is "blue". However, his witnesses must also be discounted, only 80%of the accuracy, which is also a random event (recorded B). Our problem is to find the probability of "really blue" under the condition of the witness "seeing the blue car", that is, the condition probability P (a | b). The latter should be greater than the priority probability of 15%, because the witnesses see the "blue car". How to correct the probability of first? You need to calculate p (b | a) and p (b).

Because A = blue car accident, B = witness blue, P (b | A) is the probability of "witness blue" under the condition of "blue car accident", that is, P (b | A) = 80 %. Finally, you must count the probability p (b), and its calculation is more troublesome. P (b) refers to the probability of witnesses to see a car as blue, which is equal to the probability of two situations: one is the car as blue, and the identification is correct; the other is the car green Blue. so:

From Bayesian formula:

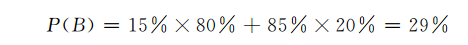
It can be counted as a 41%probability of a blue vehicle under the condition of witnesses. At the same time, the probability that the vehicle of the accident is 59%. The conditional probability of 41%greater than the priority after the revised "accident is blue", but the probability of green is 0.59 less than the green.

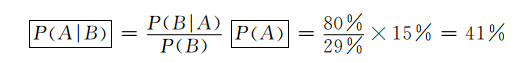
Back to the example of Wang Hong testing a certain disease, it is not difficult to get the correct answer:

A: Wang Hong in the general population is infected with some kind of disease

B: Positive results

P (A): The probability of infection with a certain disease in the general population P (B ｜ A): The correct rate of positive results

P (A | B): With the condition of positive results, Wang Hong's probability of infection with certain diseases

P (b): The total possibility of the result is positive = check the positive positive+check the true positive in the negative

Reprinted content only represents the author's point of view

Does not represent the position of the Institute of Physics of the Chinese Academy of Sciences

If you need to reprint, please contact the original public account

Source: Original Reading

Edit: Muyu

- END -